数据结构:排序算法总结
- Qingfeng Zhang
- Algorithm
- April 24, 2020
Sections
算法比较
| 排序算法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 插入排序 | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 |
| 希尔排序 | O(n^{1.3}) | O(n^2) | O(n) | O(1) | 不稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(nlog_2^n) | O(nlog_2^n) | O(nlog_2^n) | O(1) | 不稳定 |
| 冒泡排序 | O(n^2) | O(n^2) | O(n) | O(1) | 稳定 |
| 归并排序 | O(nlog_2^n) | O(nlog_2^n) | O(nlog_2^n) | O(n) | 稳定 |
| 快速排序 | O(nlog_2^n) | O(n^2) | O(nlog_2^n) | O(nlog_2^n) | 不稳定 |
| 计数排序 | O(n+k) | O(n+k) | O(n+k) | O(n+k) | 稳定 |
| 桶排序 | O(n+k) | O(n^2) | O(n) | O(n+k) | 稳定 |
| 基数排序 | O(n*k) | O(n*k) | O(n*k) | O(n+k) | 稳定 |
算法实现
插入排序
插入排序的基本思想是每一步将一个待排序的数据插入到前面已经排好序的有序序列中,直到插入完所有的元素;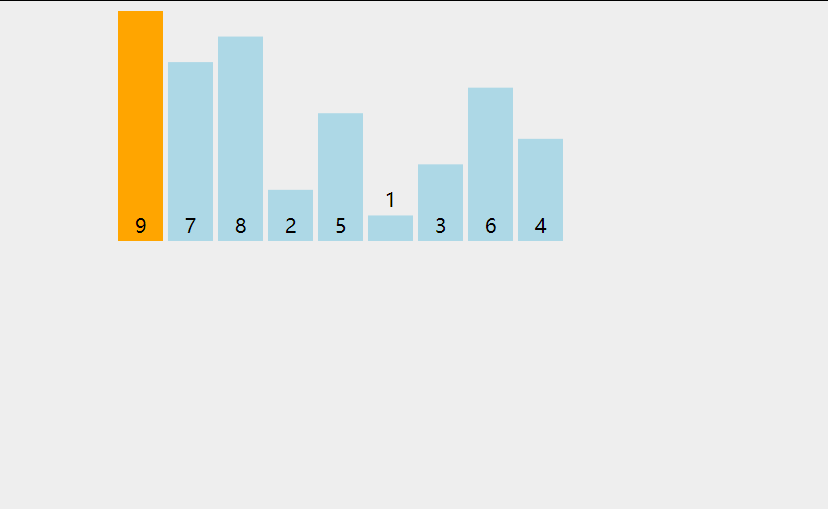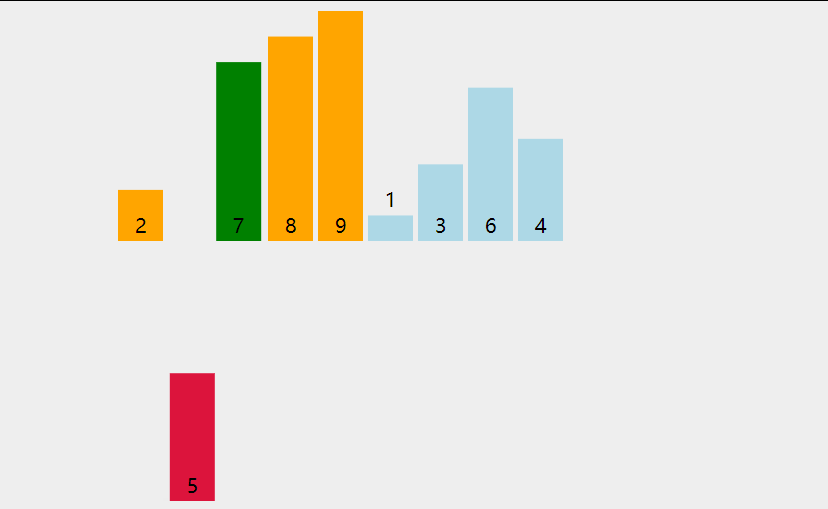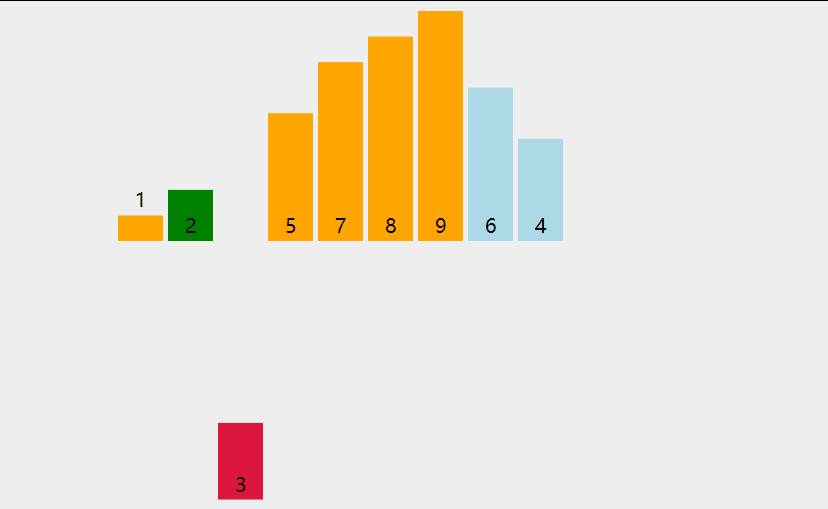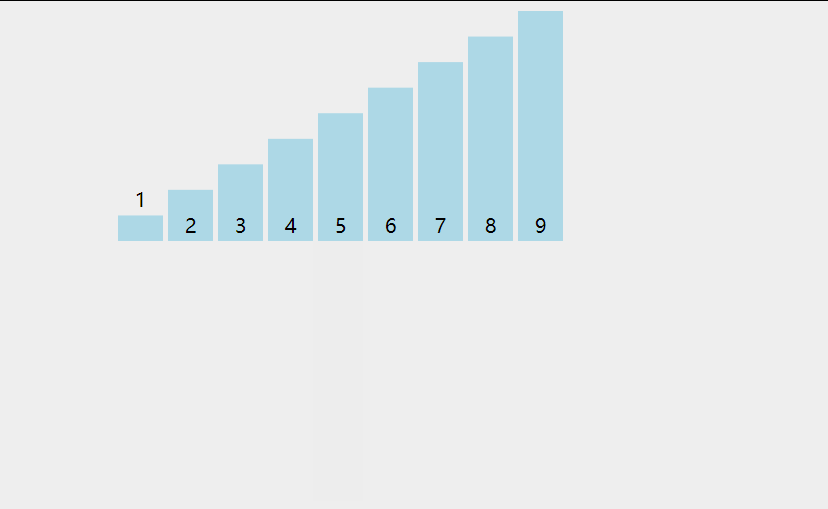
- 算法描述
1.从数组的第二个元素开始往前比较,如果比前面的数小就交换位置;
2.遍历将每个元素往前比较,直到数据全部排序完;
public class Insert {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] nums = new int[n];
for(int i=0;i<n;i++){
nums[i] = sc.nextInt();
}
InsertSort(nums);
}
public static void InsertSort(int[] nums){
for(int i=1;i<nums.length;i++){
int j = i;
while(j>0 && nums[j]<nums[j-1]){
int tmp = nums[j];
nums[j] = nums[j-1];
nums[j-1] = tmp;
j--;
}
}
}
}
冒泡排序
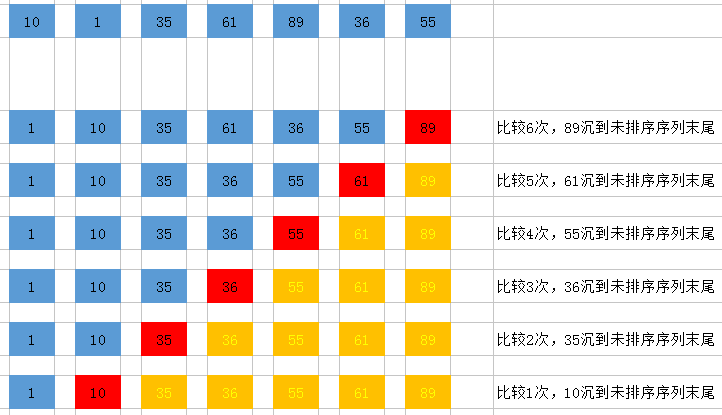
冒泡排序直观的理解就是每次将较大的数下沉到数组后面,较小的数冒出到数组前面,每次可以将最大的数放在最后一个位置,则下一次冒泡就不考虑这个数,依次迭代直到所有的数都放在正确的位置;
- 算法描述:
1.比较第1,2个元素,如果前者更大,则交换;
2.比较第2,3个元素……遍历到最后完成一趟冒泡,此时最后一个元素是最大值;
3.第二趟冒泡,比较次数减一,将第二大的值放在倒数第二个位置;
4.依次执行,每次冒泡比较的次数减一……
public class Bubble {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] nums = new int[n];
for(int i=0;i<n;i++){
nums[i] = sc.nextInt();
}
bubbleSort(nums);
}
public static void bubbleSort(int[] nums){
for(int i=0;i<nums.length-1;i++) {
boolean sign = true; //可以设置一个标志位表明数组是否已经有序
for (int j = 0; j < nums.length-i-1; j++) {
if (nums[j] > nums[j + 1]) {
int tmp = nums[j];
nums[j] = nums[j + 1];
nums[j + 1] = tmp;
sign = false;
}
}
if(sign) return ;
}
}
}
归并排序
归并排序(merge-sort)是利用归并思想实现的排序算法,采用分治策略,将问题分成一些小问题进行求解,然后将结果进行合并;
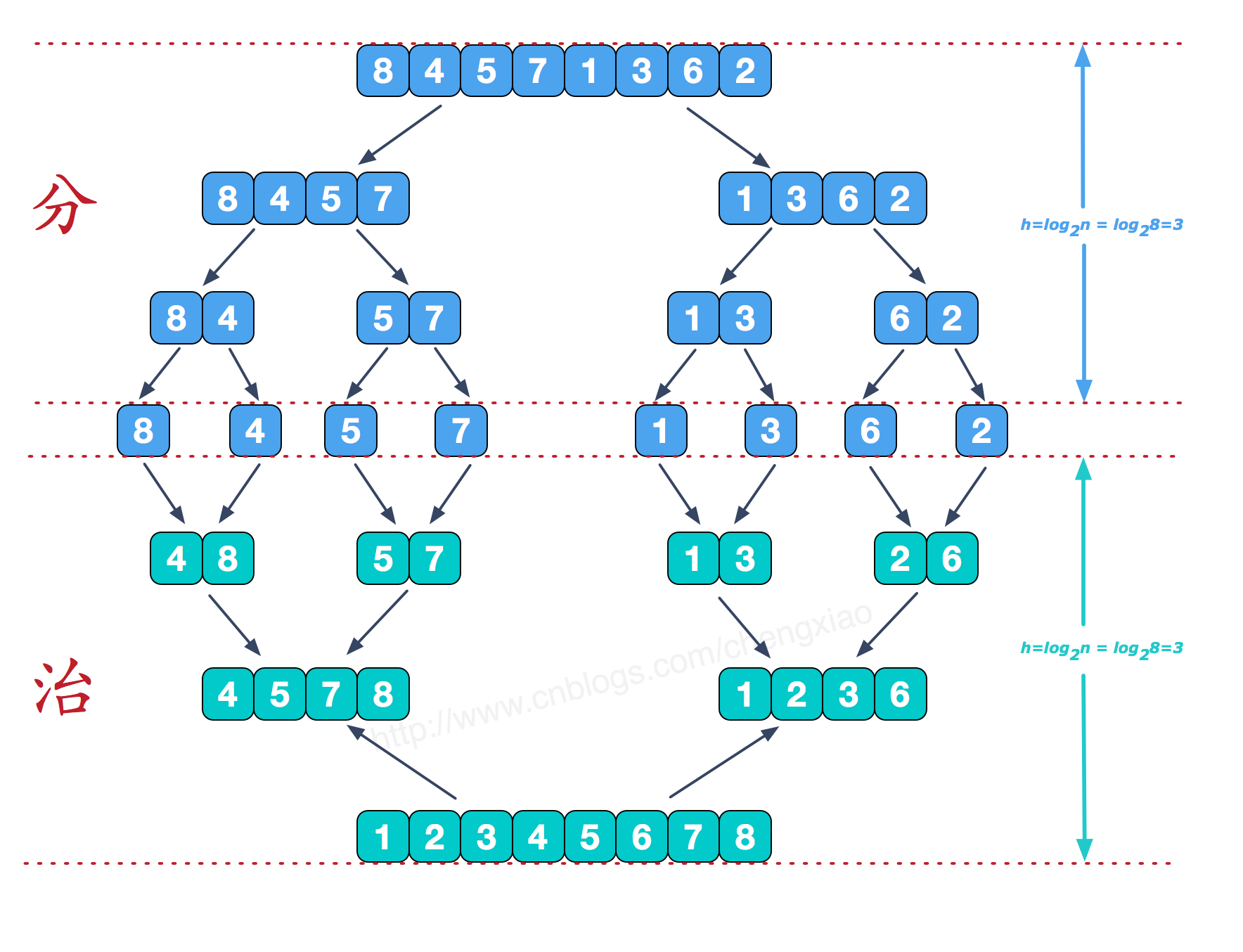
每次的合并都是合并两个有序数组:

实现细节:
- 使用DivideAndCombine方法进行递归,实现分治策略,每次将数组分两半;
- 需要使用一个临时数组用于暂存两个子数组归并之后的有序结果,并且还要复制回原数组;
- 每次都是对两个有序子数据进行归并,用两个指针指向数组最左端进行比较;
import java.util.*;
public class Merge {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int[] nums = new int[n];
for(int i=0;i<n;i++){
nums[i] = sc.nextInt();
}
mergeSort(nums);
}
public static void mergeSort(int[] nums){
int[] tmp = new int[nums.length];
DivideAndCombine(nums,tmp,0,nums.length-1);
}
public static void DivideAndCombine(int[] nums,int[] tmp,int l,int r){
if(l>=r) return ;
int mid = (r-l)/2+l;
DivideAndCombine(nums, tmp, l, mid);
DivideAndCombine(nums, tmp, mid + 1, r);
//进行有序数组的合并
int x = l, y = mid + 1; //x,y分别指向两个有序数组的左边界
int cur = l; //cur指向临时数组
while(x<=mid && y<=r){
if(nums[x]<nums[y]){ //每次将两个数组的最小值赋给tmp[cur]
tmp[cur++] = nums[x++];
}else{
tmp[cur++] = nums[y++];
}
}
while(x<=mid) tmp[cur++] = nums[x++]; //右数组先归并完
while(y<=r) tmp[cur++] = nums[y++]; //左数组先归并完
//将两个子数组的归并排序结果复制到原数组
cur = l;
while(cur<=r) {
nums[cur] = tmp[cur++];
}
}
}
LeetCode的
剑指offer51.数组中的逆序对和NO.315 计算右侧小于当前元素的个数就是利用归并排序求数组中逆序对的数量;
快速排序
快速排序的思想是通过一趟排序将待排的记录分隔为两部分,其中一部分的关键字均比另一部分的小,再对两部分分别进行快速排序,最终达到整个序列有序;
每次将序列中的最左元素作为基准数,使得基准数大于左边的所有关键字,且小于右边的所有关键字,下图是基准数为23的一趟快速排序:
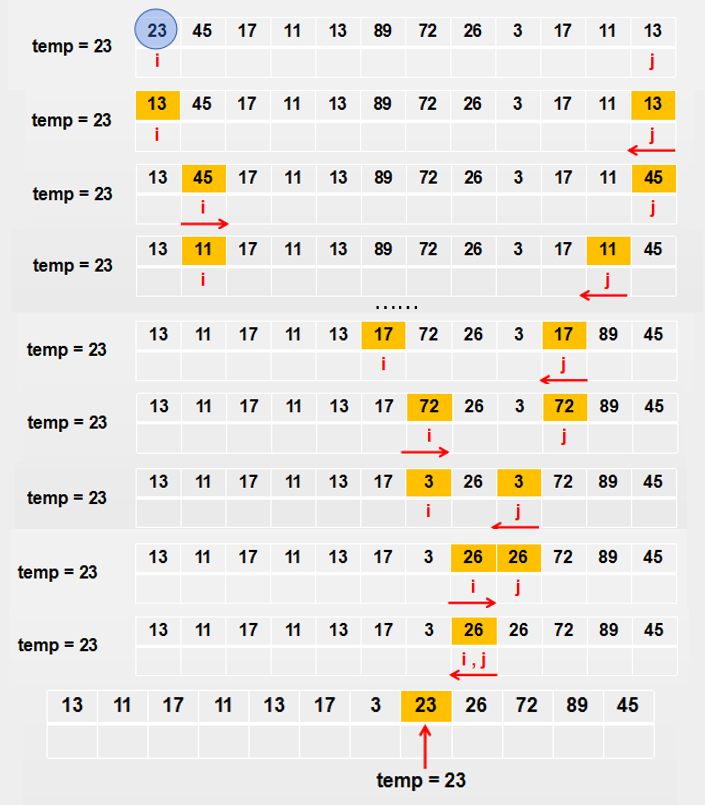
最终基准数23可以将原数组分为两个序列,然后分别对两个序列进行快速排序;
import java.util.*;
class Main {
public static void main(String[] args){
int[] nums = {3,6,3,1,6,8,1,2,5,9};
sort(nums);
System.out.println(Arrays.toString(nums));
}
public static void sort(int[] nums){
quickSort(nums,0,nums.length-1);
}
public static void quickSort(int[] nums,int left,int right){
if(left>right) return ;
int base = nums[left]; //以左边元素为基准数
int l = left, r = right;
while(l<r){
while(l<r && base<=nums[r]) r--; //从右往左找到小于base的数
nums[l] = nums[r]; //放到左边
while(l<r && base>=nums[l]) l++; //从左往右找到大于base的数
nums[r] = nums[l]; //放到右边
}
nums[l] = base; //放置base,左边均小于base,右边均大于base
quickSort(nums,left,l-1); //对base左边进行快排
quickSort(nums,l+1,right); //对base右边进行快排
}
}
LeetCode的
面试题40. 最小的k个数用到了快排的partition思想;