最小生成树算法
- Qingfeng Zhang
- Data structure
- August 15, 2020
Sections
最小生成树问题一般定义为:一个有n个节点的连通图的生成树是原图的极小连通子图,且包含原图中的所有n个节点,并且保持图连通的边的权值和最小;
构建最小生成树的算法有prim算法 和kruskal算法 ;
定义一个无向连通图如下:
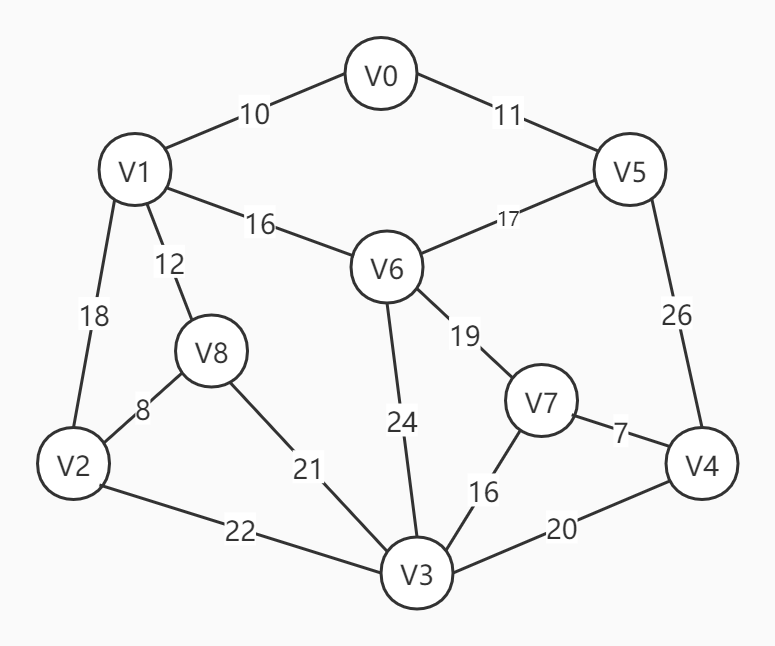
图的表示方法有邻接矩阵和邻接表;
prim算法
- 假设V是所有节点的集合,先选取一个初始节点加入集合U
- 选择以这个节点为起点的最小权值边,将终点加入U
- 每次选择起点在U中,终点在V-U中且权值最小的边
- 直到所有节点连通
选择使用邻接矩阵构造最小生成树的prim算法:
public class prim {
public static void main(String[] args) {
int sum = 0; //最小生成树的权值之和
final int M = Integer.MAX_VALUE;
//1.构造图的邻接矩阵(问题一般会给出每条边的信息,这里假设是一个无向图)
int[][] weight = {{ 0,10, M, M, M,11, M, M, M},
{10, 0,18, M, M, M,16, M,12},
{ M,18, 0,22, M, M, M, M, 8},
{ M, M,22, 0,26, M, M,16,21},
{ M, M, M,20, 0,26, M, 7, M},
{11, M, M, M,26, 0,17, M, M},
{ M,16, M, M, M,17, 0,19, M},
{ M, M, M,16, 7, M,19, 0, M},
{ M,12, 8,21, M, M, M, M, 0}
};
//2.选择一个初始节点,并初始化数组edge
// edge中存放的是当前可以选择的最小权值的边
int[] edge = weight[0];
//3.每次添加一条最小权值的边
for(int i=0;i<edge.length;i++){
//4.每次从edge中选出最小权值的边
int k = -1, minv = M; //i-k这条边的权值最小,且最小权值为minv
for(int j=0;j<edge.length;j++){
if(edge[j]>0 && edge[j]!=M){ //如果节点j与i相连
if(edge[j]<minv){ //并且i-j的权值小于minv
k = j; //更新k为节点j
minv = edge[j]; //更新最小权值
}
}
}
//5.判断最小权值边是否存在
if(k==-1) break;
//6.找到了节点k使得i-k这条边是当前所选的
sum += edge[k];
//7.更新当前可选的最小权值边edge
// 因为加入了节点k,所以可选的边也增加了weight[k]
// 对于weight[k]和edge,取每个位置最小值赋edge
for(int j=0;j<edge.length;j++){
edge[j] = Math.min(weight[k][j],edge[j]);
}
}
System.out.println(sum);
}
}
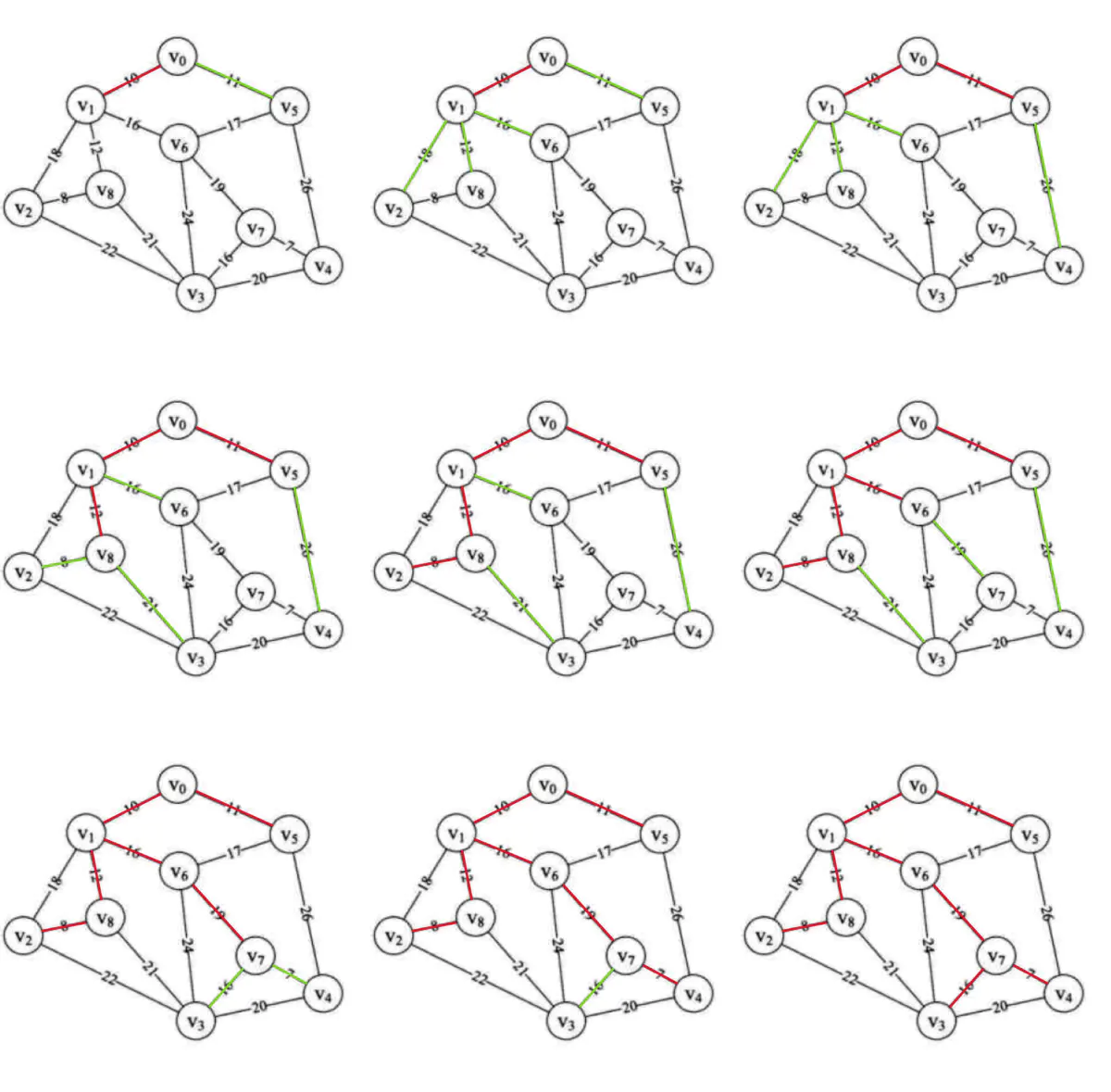
构造的过程如下图所示:
- 绿色的边是数组edge中存放的可用的边;
- 红色的边是选取的最小权值的边;
kruskal算法
- 将所有边的权值从小到大排序
- 每次选取权值最小的边,如果此边构成回路则无效,否则就是有效边
- 遍历完所有边即得到最小生成树
选择使用邻接表构造最小生成树的kruskal算法:
import java.util.*;
public class kruskal {
public static void main(String[] args) {
int sum = 0; //最小生成树的权值之和
int[][] edges = {{0,1,10},
{0,5,11},
{1,2,18},
{1,6,16},
{1,8,12},
{2,3,22},
{2,8,8},
{3,4,20},
{3,6,24},
{3,7,16},
{3,8,21},
{4,5,26},
{4,7,7},
{5,6,17},
{6,7,19}
};
//1.将所有的边按照权值从小到大排序
Arrays.sort(edges,(o1,o2)->o1[2]-o2[2]);
//2.数组arr[i]表示存在边i-end[i]
int[] arr = new int[9]; //9个节点
//3.遍历每一条边
for(int[] edge: edges){
//4.找到这条边起点和终点的代表节点
int start = find(arr,edge[0]);
int end = find(arr,edge[1]);
if(start!=end){
//5.如果两个节点不在同一个连通分量中
arr[start] = end;
sum += edge[2];
}
}
System.out.println(sum);
}
//找到x的代表节点
private static int find(int[] arr, int x){
while(arr[x]>0){
x = arr[x];
}
return x;
}
}
注意,在遍历到边0-5的时候,find(0)=1,find(5)=5,这时候出于代码实现的考虑 在arr中记录1-5,而实际的图中并没有1-5这条边,并且此时生成树添加的边也是0-5;
代表节点的思想有点类似并查集;
构造的过程如下图所示:
- 绿色的边是找到的权值最小但是是同一个连通分量的边;
- 红色的边是选取的最小权值的边;

算法分析
- prim算法的时间复杂度是 O(n^2) ,n是节点的个数,与边的数量无关,适合求边稠密图的最小生成树;
- kruskal算法的时间复杂度是 O(eloge) ,e是边的个数,与节点的数量无关,适合求稀疏图的最小生成树;~