NO.84&85 柱状图中的最大矩形问题
- Qingfeng Zhang
- Algorithm
- September 29, 2020
Sections
先从一个简化的问题说起,给定一个数组,数组中的每个数表示这个位置上的柱子高度:

现在要求的是可以在这些柱子中放下的最大矩形面积,最简单的想法就是将每个柱子作为矩形的高度,然后找找个矩形的宽度,从而计算面积; 更巧妙的方法是使用单调栈求解,单调栈是保证栈中元素递增或者递减的一个栈,递增的单调栈可以保证先出栈的值大于后出栈的值,从而保证矩形的高度至少为后出栈的元素值大小;
- 每次判断当前的高度是否大于栈顶数对应的高度,如果是则将索引(便于计算矩形宽度)入栈;
- 否则将所有小于当前高度的索引出栈,同时计算面积,取最大值;
- 将当前数的索引入栈;
- 最后将所有数出栈,同时计算面积,取最大值;
单调栈连续出栈计算矩形面积的过程如下图所示:
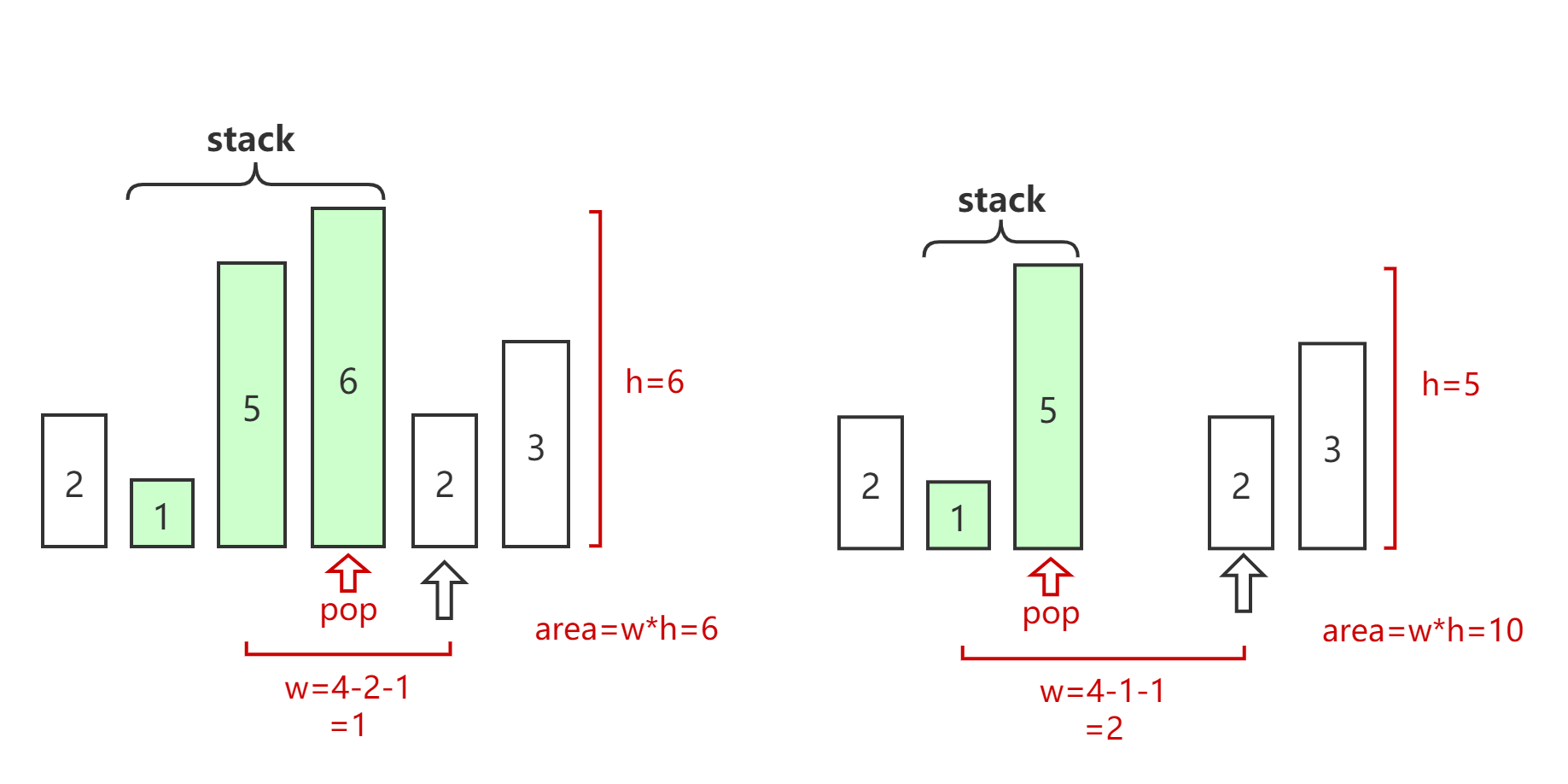
NO.84 柱状图中最大的矩形
class Solution {
public int largestRectangleArea(int[] heights) {
if(heights.length==0) return 0;
int res = 0;
Deque<Integer> stack = new LinkedList<>();
stack.push(0);
int p = 1;
while(p<heights.length){
while(!stack.isEmpty() && heights[p]<heights[stack.peek()]){ //如果高度小于栈顶元素的高度,则出栈
int h = heights[stack.pop()];
int w = stack.isEmpty()?p:p-stack.peek()-1;
res = Math.max(res,h*w);
}
stack.push(p++);
}
while(!stack.isEmpty()){ //奖所有元素出栈,计算面积
int h = heights[stack.pop()];~
int w = stack.isEmpty()?p:p-stack.peek()-1;
res = Math.max(res,h*w);
}
return res;
}
}
还有一个常见的问题:求一个0-1矩阵中构成的最大矩形面积,这个问题第一眼看像是动态规划问题,但是如果真的用动态规划求解,则对于每个位置都将其作为左上角,然后再计算dp矩阵,时间复杂度过高;
其实这个问题和NO.84几乎一样,就是将矩阵中连续的1看作柱子,对于每一行,计算以这行为底部的柱子的高度数组,然后就是NO.84的问题了;
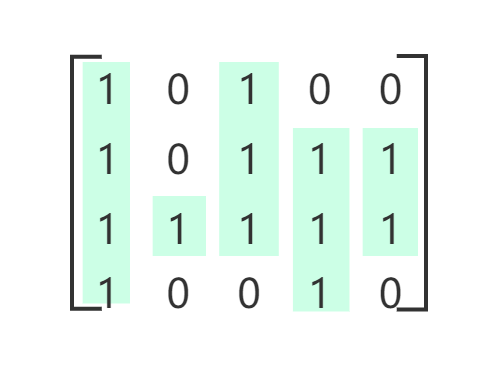
NO.85 最大矩形
class Solution {
public int maximalRectangle(char[][] matrix) {
int res= 0;
for(int i=0;i<matrix.length;i++){
int[] heights = new int[matrix[0].length];
for(int k=0;k<heights.length;k++){
int p = i;
while(p>=0 && matrix[p--][k]=='1'){
heights[k]++;
}
}
int area = largestRectangleArea(heights);
res = Math.max(res,area);
}
return res;
}
public int largestRectangleArea(int[] heights) {
if(heights.length==0) return 0;
int res = 0;
Deque<Integer> stack = new LinkedList<>();
stack.push(0);
int p = 1;
while(p<heights.length){
while(!stack.isEmpty() && heights[p]<heights[stack.peek()]){
int h = heights[stack.pop()];
int w = stack.isEmpty()?p:p-stack.peek()-1;
res = Math.max(res,h*w);
}
stack.push(p++);
}
while(!stack.isEmpty()){
int h = heights[stack.pop()];
int w = stack.isEmpty()?p:p-stack.peek()-1;
res = Math.max(res,h*w);
}
return res;
}
}