Leetcode算法题集(Java)
- Qingfeng Zhang
- Algorithm
- December 13, 2019
Sections
2019年12月13日,Leetcode上数组部分的简单题已经用java做完,在接下来做动态规划的简单题和继续做数组之间我选择了后者,因为没必要一直揪着简单题,越是怕就越要把它做掉。虽然之前也没有写几篇题解,但这里还是新开了一篇用来记录做中等题的题解。
1. 多数和问题
最近两天连续做到关于多数和的问题,一般是给定一个数组nums和一个目标数target,找出数组中三个数(或四个数)的和等于target的所有结果,也有一些问题会不要求相等,只要求最接近;
第一次做是用Python写的,但是完全没头绪,两数和、三数和,现在又来个四数和。。。但是做过之后,现在再做就很简单了,因为基本就一个思路:先排序,套循环结构,最后两个循环可以用前后双指针代替
,如果不用双指针的话,三数和的时间复杂度就是 O(n^3) ,四数和的时间复杂度是 O(n^4)
,这样做的话铁定超时,所以要先排序,对排序后的数组用前后双指针,当前后指针所指的数之和大于目标值
(一般是target减去前去一个或两个数),就令r--,如果小于目标值 ,就令l++;
NO.15 三数之和
题目和上述的一样,在nums中找三个数的和等于target,找出所有的三元组,不能重复,返回一个二维List;
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> result = new ArrayList<>();
for(int i=0;i<nums.length-2;i++){
int tmp = -nums[i];
int l=i+1, r=nums.length-1;
while(l<r){
if(nums[l]+nums[r]==tmp){
List<Integer> L = new ArrayList<>();
L.add(nums[i]);
L.add(nums[l++]);
L.add(nums[r--]);
if(!result.contains(L)){result.add(L);}
}else if(nums[l]+nums[r]>tmp){r--;}
else{l++;}
}
}
return result;
}
}
NO.16 最接近的三数之和
在nums中找到三个数的和与target最接近,返回这三个数的和;
class Solution {
public int threeSumClosest(int[] nums, int target) {
Arrays.sort(nums);
int min = Integer.MAX_VALUE;
int sum = 0;
for(int i=0;i<nums.length-2;i++){
int l=i+1, r=nums.length-1;
int tmp = target-nums[i];
while(l<r){
if(min>Math.abs(nums[l]+nums[r]-tmp)){
sum = nums[i]+nums[l]+nums[r];
min = Math.abs(nums[l]+nums[r]-tmp);
}
if(nums[l]+nums[r]<tmp){l++;}
else if(nums[l]+nums[r]>tmp){r--;}
else{return sum;}
}
}
return sum;
}
}
NO.18 四数之和
在nums中找到四个数和等于target,找到所有的四元素,不能重复,返回一个二维List;
class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
Arrays.sort(nums);
List<List<Integer>> result = new ArrayList<>();
for(int i=0;i<nums.length-3;i++){
for(int j=i+1;j<nums.length-2;j++){
int l=j+1, r=nums.length-1;
while(l<r){
int tmp = nums[i]+nums[j]+nums[l]+nums[r];
if(tmp==target){
List<Integer> L = new ArrayList<>();
L.addAll(Arrays.asList(nums[i],nums[j],nums[l++],nums[r--]));
if(!result.contains(L)){result.add(L);}
}else if(tmp<target){l++;}
else{r--;}
}
}
}
return result;
}
}
2. 搜索旋转数组问题
这类问题一般是给定一个排序数组,但是这个数组会在某一点进行旋转,比如数组[1,2,3,4,5,6,7,]在3这一点进行旋转得到[4,5,6,7,1,2,3],要求在旋转后的数组内进行搜索,判断一个数target是否存在,一般这类问题会要求时间复杂度为O(logn),一开始做的时候是先找到旋转点,然后再二分查找,但是想想才发现这和顺序查找有什么区别?这种问题首先会考虑使用二分法进行查找;
NO.33 搜索旋转排序数组
给定一个不包含重复元素的旋转数组nums和目标值target,判断nums中是否包含target,包含则返回索引,否则返回-1;
既然是旋转过的排序数组那就是无序了,那就不能套用一般的二分法,但是还是局部有序的,因此可以对二分策略进行讨论:
对于原数组为[1,2,3,4,5,6,7],有两种旋转情况:
情况1:[5,6,7,1,2,3,4];
情况2:[4,5,6,7,1,2,3];
按照二分法的策略,设置左右指针分别指向头尾,即nums[l]和nums[r],mid指针指向中间nums[(l+r)/2];
对于情况1,nums[l]>nums[mis],mid的右边有序,因此右边最大值为nums[r],最小值为nums[l];对于情况2,nums[l]<nums[mid],mid的左边有序,因此左边最大值为nums[mid],最小值为nums[l];
(用nums[mid]和nums[r]进行比较也一样,其实就是如果nums[j]>nums[i],则从i到j是递增的)
根据mid一侧的最大最小值就可以判断target是否在这边,否则就在另一边,由此更新mid的值,从而达到二分法的效果;
class Solution {
public int search(int[] nums, int target) {
int l=0, r=nums.length-1;
while(l<=r){
int mid = (l+r)/2;
if(nums[mid]==target) return mid;
if(nums[l]>nums[mid]){
if(nums[mid]<target && nums[r]>=target){
l = mid+1;
}else{r = mid-1;}
}else{
if(nums[l]<=target && nums[mid]>target){
r = mid-1;
}else{l = mid+1;}
}
}
return -1;
}
}
NO.81 搜索旋转排序数组II
这题与上一题的区别在于nums中可能存在重复的值,因此基于上一题的分析需要多考虑一种情况,也就是nums[l]==nums[mid]的情况,对于数组[0,1,1,1,1],假设其旋转的情况如下:
情况3:[1,0,1,1,1];
此时,nums[l]==nums[mid],无法判断mid的左边还是右边有序,对于这种情况只要l++就行,因为此时mid右边的值都与nums[mid]相等,而mid左边可能存在不等的值;
class Solution {
public boolean search(int[] nums, int target) {
int l=0, r=nums.length-1;
while(l<=r){
int mid = (l+r)/2;
if(nums[mid]==target) return true;
if(nums[l]==nums[mid]){ //对于这种情况,令r--没用,这也是为什么后面将nums[l]和nums[mid]进行比较
l++;
continue;
}
if(nums[l]<nums[mid]){ //mid的左边有序
if(nums[l]<=target && target<nums[mid]){ //有序所以可以判断target是否在左边
r = mid-1;
}else{l=mid+1;} //否则在右边
}else if(nums[l]>nums[mid]){ //mid的右边有序
if(nums[mid]<target && nums[r]>=target){ //同上,可以判断target是否在右边
l = mid+1;
}else{r=mid-1;} //否则在左边
}
}
return false;
}
}
NO.153 寻找旋转排序数组中的最小值
这道题有点不一样:在旋转数组中找出最小值,当然可以用O(n)的方法来做,但是这明显不是题目的本意,要利用旋转数组局部有序的性质,因此还是用二分法;
class Solution {
public int findMin(int[] nums) {
int l=0, r=nums.length-1;
if(nums.length==1) return nums[0];
if(nums.length==2) return nums[0]<nums[1]?nums[0]:nums[1];
while(l<=r){
int mid = (l+r)/2;
if(nums[l]<nums[r]) return nums[l];
if(nums[mid]<nums[mid-1]) return nums[mid];
else if(nums[mid]<nums[l]) r = mid;
else l = mid+1;
}
return -1;
}
}
以上的解法也是基于二分法,但是感觉有点繁琐,因此有一个改进的更巧妙的方法:
class Solution {
public int findMin(int[] nums) {
int l=0, r=nums.length-1;
while(l<r){
int mid = (l+r)/2;
if(nums[mid]>nums[r]){l = mid+1;} //如果mid左边不是有序,则左边包含最小值,且nums[mid]不是最小值
else{r = mid;} //否则最小值在右边,nums[mid]可能是最小值
}
return nums[l];
}
}
这里的二分策略与一般的二分法的区别仅在于l<r和r=mid,因为每次要找到包含最小值的一边,如果nums[mid]<nums[r],说明右边有序且不包含最小值,并且nums[mid]可能是最小值,因此令r=mid;如果nums[mid]>nums[r],说明最小值就在右边,且nums[mid]一定不是最小值,因此令l=mid+1;
NO.154 寻找旋转排序数组中的最小值II
这道题与上一题的唯一区别就是包含重复值,因此在上一题的基础上多考虑一种情况,也就是nums[mid]==nums[r],此时根据l和r的位置无法判断最小值是在哪一边,因此,如果l右边数不变可以令l++,如果r左边的数不变可以令r–(其实也可以直接令r–,参考NO.81);
class Solution {
public int findMin(int[] nums) {
int l=0, r=nums.length-1;
while(l<r){
int mid = (l+r)/2;
if(nums[mid]==nums[r]){
if(nums[r]==nums[r-1]){r--;}
if(nums[l]==nums[l+1]){l++;}
}
else if(nums[mid]>nums[r]){l=mid+1;}
else{r=mid;}
}
return nums[l];
}
}
3. 丑数问题
丑数的定义是只包含质因数2,3,5的正整数;
NO.263 丑数
判断一个给定的数是否为丑数;
这是一道简单题,但是如果暴力求解还是不好计算的,需要找出其每个因数并判断是否为质数,其实只需要“除掉”这个数中的2,3,5即可:
class Solution {
public boolean isUgly(int num) {
if(num<1) return false;
while(num%2==0){
num /= 2;
}
while(num%3==0){
num /= 3;
}
while(num%5==0){
num /= 5;
}
return num==1;
}
}
NO.264 丑数II
丑数是因数里只包含2,3,5的正整数,认为1也是丑数,求第n个丑数;
第一眼看到就觉得这是一个一般的动态规划问题,dp[i]可以由dp[i/2],dp[i/3],dp[i/5]求得(如果可以整除),但是如果用数组,事先又不知道数组长度,因为有非丑数,如果用ArrayList或HashSet又会超时,难办。。。
有一个很妙但是又感觉很普通(为什么自己没有想到)的方法:三指针,使用三个指针,每次取三个指针分别乘以2,3,5中的最小结果,即是下一个丑数,然后将取得最小结果的指针后移一位,感觉像是上面的想法倒过来实现,只是每次要保证得到的是最小的丑数:
class Solution {
public int nthUglyNumber(int n) {
// if(n==1) return 1;
// int count = 1, i = 2;
// int[] factor = {2,3,5};
// List<Integer> l = new ArrayList<>();
// l.add(1);
// l.add(1);
// while(count<n){
// l.add(0);
// for(int num: factor){
// if(i>=num && i%num==0 && l.get(i/num)==1){
// l.set(l.size()-1,1);
// count++;
// break;
// }
// }
// i++;
// }
// return l.size()-1;
int a=0, b=0, c=0;
int[] arr = new int[n];
arr[0] = 1;
for(int i=1;i<n;i++){
int ugly = Math.min(arr[a]*2,Math.min(arr[b]*3,arr[c]*5));
arr[i] = ugly;
if(arr[i]==arr[a]*2) a++;
if(arr[i]==arr[b]*3) b++;
if(arr[i]==arr[c]*5) c++;
}
return arr[n-1];
}
}
4. 字符串问题
字符串问题本来是一大类问题,和数组一样,但是目前做题遇到的方法不多,就暂时将字符串问题分为一类;
NO.3 无重复字符的最长子串
给定一个字符串,找出其中不含重复字符的最长子串,就和题目名字一样;最简单的方法就是遍历字符串,每次将遍历过的字符放到一个HashSet里,遍历到新的字符,判断HashSet里有没有重复字符,如果有,找到这个字符在字符串中的位置,并且从这个位置开始新一轮的遍历;
class Solution {
public int lengthOfLongestSubstring(String s) {
int i=0, count=0;
while(i<s.length()){
Set<Character> set = new HashSet<>();
int j=i;
while(j<s.length() && !set.contains(s.charAt(j))){
set.add(s.charAt(j++));
}
count = Math.max(count,set.size());
if(j==s.length()) return count; //因为遍历到末尾结束
while(s.charAt(i)!=s.charAt(j)){
i++; //因为遇到重复元素才结束
}
i++;
}
return count;
}
}
方法二:滑动窗口 ,双指针分别指向字符串中滑动窗口的前后,每次将后面指针的元素加入到HashSet,如果元素重复,就将前面指针的元素从HashSet里删掉,期间,记录HashSet的最大大小:
class Solution {
public int lengthOfLongestSubstring(String s) {
int i=0, j=0, ans=0;
Set<Character> set = new HashSet<>();
while(i<s.length() && j<s.length()){
if(!set.contains(s.charAt(j))){
set.add(s.charAt(j++));
ans = Math.max(ans,set.size());
}else{
set.remove(s.charAt(i++));
}
}
return ans;
}
}
方法三:改进的滑动窗口 ,将遍历过的元素及其位置放入HashMap中,也就是方法一的思想,重复元素之间的元素就不用遍历了,利用HashMap直接跳到重复元素的位置:
class Solution {
public int lengthOfLongestSubstring(String s) {
Map<Character, Integer> map = new HashMap<>();
int i=0, ans=0;
for(int j=0;j<s.length();j++){
if(map.containsKey(s.charAt(j))){
i = Math.max(map.get(s.charAt(j))+1,i); //要取i和前面一个重复元素位置的最大值
}
ans = Math.max(ans,j-i+1);
map.put(s.charAt(j),j); //已存在的key会更新value为最大值
}
return ans;
}
}
NO.5 最长回文子串
这道题比较有意思,给定一个字符串,找出其中长度最长的回文子串,回文子串就是反转后与自己相等,但是要在一个长字符串中找到一个回文子串,同时要求长度最大;像这种实际中很常见,但是作为算法题一下又想不出比较简单有效的方法的问题是值得记录一下的;
方法一:暴力求解 ;一下子想不出好的方法,那就先用暴力求解试试呗,将每个子串都判断一下是否是回文串,最后。。。当然是超时了:
class Solution {
public String longestPalindrome(String s) {
int ans = 0;
String result = "";
for(int i=0;i<s.length()-ans;i++){
for(int j=i;j<s.length();j++){
if(j-i+1>ans && judge(s.substring(i,j+1))){
ans = j-i+1;
result = s.substring(i,j+1);
}
}
}
return result;
}
public boolean judge(String s){
StringBuilder sb = new StringBuilder(s);
sb.reverse();
return s.equals(sb.toString());
}
}
方法二:动态规划 ;没想到这道题也可以用动态规划,需要一个二维的dp数组(好像可以优化内存),令dp[i,j]表示从下标i到j子串的子串是否是回文串(1/0),对于dp[i,j]的更新就可以表示为:
dp[i,j]= \begin{cases} 1 \ \ ,if \ dp[i+1,j-1]==1 \ and \ s[i]==s[j] \\ 0 \
,otherwise \\ \end{cases}
对于dp数组,只需要更新对角线以及右上角的部分,记录dp[i,j]==1中j-i+1的最大值的同时也要记录子串的位置:
class Solution {
public String longestPalindrome(String s) {
if(s.length()==0) return s;
int[] ans = {0,0};
int[][] dp = new int[s.length()][s.length()];
for(int k=0;k<s.length();k++){
for(int i=0;i<s.length()-k;i++){
if(i+1>i+k-1 || dp[i+1][i+k-1]==1){
dp[i][i+k] = s.charAt(i)==s.charAt(i+k)?1:0;
}
if(dp[i][i+k]==1 && k+1>ans[1]-ans[0]+1){
ans[0] = i;
ans[1] = i+k;
}
}
}
return s.substring(ans[0],ans[1]+1);
}
}
方法三:中心扩展法 ;遍历字符串,将遍历到的位置作为回文子串的中心,然后由中心向外扩展,从到找到以当前位置为中心的最长回文子串,但是回文子串的长度会有奇数和偶数两种情况,因此每次扩展的中心也要考虑两种情况:
class Solution {
public String longestPalindrome(String s) {
if(s.length()==0) return s;
int l=0, r=0;
for(int i=0;i<s.length();i++){
int[] p1 = search(s,i,i);
int[] p2 = search(s,i,i+1);
if(p1[1]-p1[0]-1>r-l-1){
l = p1[0];
r = p1[1];
}
if(p2[1]-p2[0]-1>r-l-1){
l = p2[0];
r = p2[1];
}
}
return s.substring(l+1,r);
}
public static int[] search(String s, int i, int j){
while(i>=0 && j<s.length() && s.charAt(i)==s.charAt(j)){
i--;
j++;
}
return new int[]{i,j};
}
}
NO.12 整数转罗马数字
给定一个整数(大于0小于3999),将其转换为罗马数字表示,在罗马数字中1000,500,100,50,10,5,1分别由”M”,”D”,”C”,”L”,”X”,”V”,”I”表示,特别要注意的是4,9,40,90,400,900有单独的表示”CM”,”CD”,”XC”,”XL”,”IX”,”IV”;
一开始想到的解法比较复杂,就是对整数的每一位进行判断,如果是4或9,就直接在HashMap中找到,否则判断大于5或是小于5,同时还要根据位数乘上10的倍数;
可以从最大的数1000,到900…到4,1,如果给出的数num大于这些数,就减去,然后字符串中添加这些数对应的表示,到最后num减为0,得到的字符串就是结果:
class Solution {
public String intToRoman(int num) {
int[] arr = {1000,900,500,400,100,90,50,40,10,9,5,4,1};
String[] S = {"M","CM","D","CD","C","XC","L","XL","X","IX","V","IV","I"};
StringBuilder sb = new StringBuilder();
for(int i=0;i<arr.length;i++){
while(num>=arr[i]){
num -= arr[i];
sb.append(S[i]);
}
}
return sb.toString();
}
}
NO.49 字母异位词分组
给定一个字符串数组,将字母相同但是顺序不同的字符串分为一组,如:["eat", "tea", "tan", "ate", "nat", "bat"]的分组结果为[["ate","eat","tea"],["nat","tan"],["bat"]];
首先肯定要有个方法判断两个字符串是否是异位词,我想到的方法是使用长度26的数组记录每个字母的出现次数,遍历字符串数组,得到字符串的统计数组,然后再遍历二维list,与每个list的第一个字符串的统计数组比较,如果相等,就将字符串放入到这个lsit中,但是这样做太耗时了;
还有个判断两个字符串是否是异位词的方法:对字符串进行排序;基于这个思想,可以使用一个HashMap,map的value是一个字符串list,存放原字符串数组的元素,而key是value中字符串排序的结果,以上面给出例子为例,可以得到结果:{"aet"=["ate","eat","tea"],"ant"=["nat","tan"],"abt"=["bat"]}:
class Solution {
public List<List<String>> groupAnagrams(String[] strs) {
Map<String,List<String>> map = new HashMap<>();
for(String s: strs){
char[] arr = s.toCharArray();
Arrays.sort(arr);
String key = String.valueOf(arr); //对字符串进行排序
if(!map.containsKey(key)){
map.put(key,new ArrayList<>()); //创建不存在的键值
}
map.get(key).add(s); //在key对应的value中添加字符串
}
return new ArrayList(map.values()); //将HashMap的值转换为二维List
}
}
最后将HashMap的value转换为二维listnew ArrayList(map.values())要注意一下。
NO.394 字符串解码
(这道题写的心态崩掉了)给定一个字符串,其中包括字母、数字和中括号,中括号内为字母,数字后接着中括号,如3[a2[c]],数字表示中括号内的字符串重复的次数,本题的主要问题是要考虑中括号内还可以包括中括号,因此可以使用栈来做,如果不是]就入栈,否则就在栈里找上一个[,并找出其前面的数字,将字符串重复对应次数后再入栈,最后将栈内的字符串连起来就是结果:
class Solution {
public String decodeString(String s) {
Stack<String> stack = new Stack<>();
StringBuilder result = new StringBuilder();
for(char c: s.toCharArray()){
if(c!=']'){
stack.push(c+"");
}else{
StringBuilder sb = new StringBuilder();
StringBuilder num = new StringBuilder();
while(!stack.peek().equals("[")){
sb.insert(0,stack.pop());
}
stack.pop();
while(!stack.empty() && !stack.peek().equals("[")){
num.insert(0,stack.pop());
}
stack.push(decode(num.toString(),sb.toString()));
}
}
while(!stack.empty()) result.insert(0,stack.pop());
return result.toString();
}
public String decode(String num, String s){
StringBuilder sb = new StringBuilder();
int i = 0;
while(Character.isLetter(num.charAt(i))){
sb.append(num.charAt(i++));
}
for(int j=0;j<Integer.valueOf(num.substring(i));j++){
sb.append(s);
}
return sb.toString();
}
}
NO.767 重构字符串
给定一个字符串S,对其每个元素进行重新排列,要求重排结果中没有相邻两个字符相同,如果不存在返回空串;
可以用一个字符数组来存储重排后的结果,对于这个字符数组可以是先填满数组的偶数(或奇数)位置,再填奇数(偶数)位置,并且最关键的是:
要保证出现最多的字符应该填写在奇数位置!!!
如果用hashmap或数组记录每个字符出现的次数,要先找出出现最多的字符,先将该字符填在数组里,再去考虑其它字符,比较麻烦;
有一个技巧就是,还是使用数组记录次数,但是记录完之后对数组进行排序,就可以知道出现最多的字符,但是问题是排序之后丢失了下标顺序,而字符值就是通过下标确定的,有一个很巧的方法就是将字符出现次数和下标的值存储在数组值地不同位上,如:’c’出现3次,则C[‘c’-‘a’]
= 3*100 + ‘c’; 这样可以使次数和字符值互不影响地存储;
class Solution {
public String reorganizeString(String S) {
int[] record = new int[26];
for(int i=0;i<record.length;i++){
record[i] = i; //存储每个位置对应的字符值
}
for(char c: S.toCharArray()){
record[c-'a'] += 100; //记录每个字符的出现次数*100
}
Arrays.sort(record);
// System.out.println(Arrays.toString(record));
char[] C = new char[S.length()]; //建立一个字符数组
int index = 1; //先将字符放在偶数位置
//出现次数升序排列,保证先将出现次数少的字符先放在偶数位置,然后再放奇数位置
//这样可以保证不会有相同字符相邻
for(int n: record){
char ch = (char)(n%100+'a'); //对应的字符
int count = n/100; //出现的次数
if(count>(S.length()+1)/2) return "";
for(int i=0;i<count;i++){
if(index>=C.length) index = 0; //偶数位置满了之后开始在奇数位置放
C[index] = ch;
index += 2;
}
}
return String.valueOf(C);
}
}
5. 并查集
并查集是一种精妙使用的数据结构,主要用于处理一些不相交集合的合并问题,常用于:
- 求连通子图
- 求最小生成树Kruskal算法
- 求最近公共祖先LCA
并查集的基本操作:
- make建立一个新的并查集;
- merge(x,y)如果x和y所在的集合不相交,则将其进行合并:将一个集合代表节点设置为另一个集合代表节点的父节点;
- find(x)查找节点所在集合的代表节点 ;
对于并查集的优化有路径压缩和按秩合并;
NO.684 冗余连接
给定一个二维数组表示无向图的所有边,且每条边[u,v]满足u< v,图是由一棵树和一条符加的边组成的,因此会存在环路,要求删掉一条边使得图变成一棵树;
使用并查集,先将每一个节点作为一个集合,自己就是代表节点,每加入一条边,查找边的起点和终点所在的集合的代表节点,如果两个代表节点相同,说明这两个节点已经在同一个集合中了,当前这条边就是重复的,如果两个代表节点不同,将两个集合合并;
parent[i]记录的是节点i的代表节点,也就是i在树中的父节点,如果要找到节点i所在集合的代表节点,要递归直到i=parent[i];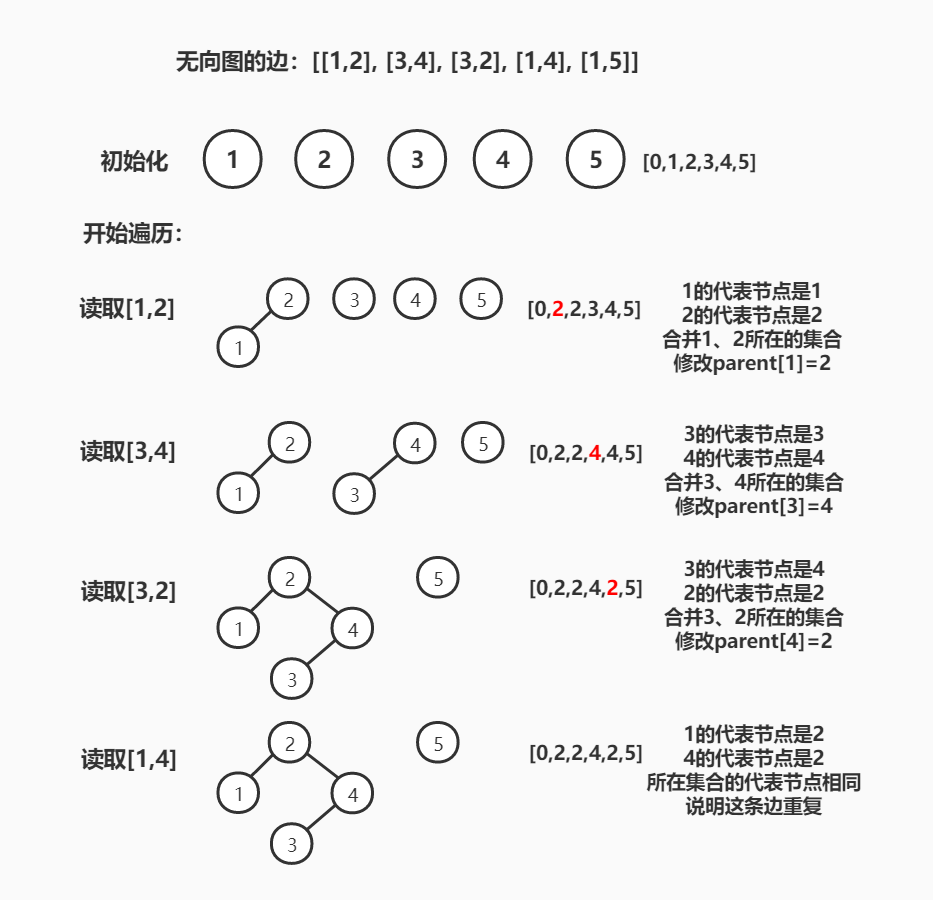
最后将[1,5]连接上就是一棵树;
class Solution {
int[] parent = new int[1001]; //parant[a]=b表示a的表示节点是b,和父节点类似
public int[] findRedundantConnection(int[][] edges) {
for(int i=0;i<parent.length;i++) parent[i] = i; //parent初始化
int[] res = new int[2];
for(int[] l: edges){
if(find(l[0])!=find(l[1])){
merge(l[0],l[1]);
}else{ //当前边的两个节点已经在同一个集合中了,此条边就是可以删掉的
res[0] = l[0];
res[1] = l[1];
}
}
return res;
}
public int find(int x){ //查找x所在集合的代表节点
while(x!=parent[x]){
x = parent[x];
}
return x;
}
public void merge(int x,int y){ //合并x和y所在的集合
int a = find(x), b = find(y);
parent[a] = b; //将x集合的代表节点放到y集合代表节点b的下面
}
}
NO.990 等式方程的可满足性
给定一个字符串数组,其中每个字符串类似”a==b”、”a!=b”的判断两个变量是否相等的形式,要求判断所有的判断语句是否合法,当存在”a==b”、”a!=b”时则矛盾不合法;
可以先根据”==”字符串构建并查集,然后再判断”!=”是否合法,也就是看”!=”两端的变量是否存在于同一个集合中;
class Solution {
int[] parent = new int[26];
public boolean equationsPossible(String[] equations) {
for(int i=0;i<parent.length;i++) parent[i] = i;
for(String s: equations){ //先根据==的字符串构造并查集
if(s.charAt(1)=='='){
merge(s.charAt(0),s.charAt(3));
}
}
for(String s: equations){ //对于!=的字符串,查看两个变量是否在同一个集合中
if(s.charAt(1)=='!'){
if(find(s.charAt(0))==find(s.charAt(3))) return false;
}
}
return true;
}
public void merge(char x,char y){
parent[find(x)] = find(y);
}
public int find(char x){
int n = x-'a';
while(n!=parent[n]) n = parent[n];
return n;
}
}
其他问题
NO.448 找到所有数组中消失的数字
题目非常简单,给定一个数组包含n个数,每个数都是1到n之间,但是里面会有重复的数,因此就有1到n的某几个数没出现,找出这几个没出现的数;
简单的解法当然也非常简单,建立一个HashSet,令i从1到n循环,如果i不在HashSet里面,就将其添加到List里,最后返回List,代码如下:
class Solution {
public List<Integer> findDisappearedNumbers(int[] nums) {
List<Integer> L = new ArrayList<>();
Set<Integer> set = Arrays.stream(nums).boxed().collect(Collectors.toSet());
for(int i=1;i<=nums.length;i++){
if(! set.contains(i)){
L.add(i);
}
}
return L;
}
}
但是题目要求不能用额外的空间,并且时间复杂度为O(n),这里用了额外的HashSet,并且查找也比较耗时;
题目里有一个很关键的点就是数组包含n个数
,想象一下,如果正好是1到n这n个数,如果将其排序,则每个元素值和其位置相同,即使将其顺序打乱,这n个元素之间也能够相互对应;
看一个例子:[4,3,2,7,8,2,3,1],数组有8个数,不包含5,6,且2,3重复,一个从1到n的数组为:
[1,2,3,4,5,6,7,8]
每个数组元素值与元素位置是一样的,因此nums[i]对应的元素就是i,而对于此问题的例子,将其排序后:
[1,2,2,3,3,4,7,8]
如果将nums[i]对应的位置的元素乘上-1(保证为负),那么最后的结果就是:
[-1,-2,-2,-3,3,4,-7,-8]
其中第5,6个元素任为正,说明数组中没有元素值为5,6的元素对应到这个位置,因此没有乘上-1;
如果这样想:将第5,6个元素换为2,3,得到的数组就为:
[1,2,3,4,2,3,7,8]
这样就可以更直观地看出为什么不包含5,6的数组映射结果中只有第5,6个元素的值大于0,之所以能够这样做,最主要的还是数组里的元素个数为n;
求解的代码如下:
class Solution {
public List<Integer> findDisappearedNumbers(int[] nums) {
for(int i: nums){
if(nums[Math.abs(i)-1]>0){
nums[Math.abs(i)-1] *= -1;
}
}
List<Integer> L = new ArrayList<>();
for(int j=0;j<nums.length;j++){
if(nums[j]>0){
L.add(j+1);
}
}
return L;
}
}
NO.1160 拼写单词
有一段时间没有写做题的笔记了,因为简单题已经用python做过一遍,该写的笔记也写过了,所以一般只在遇到比较典型的问题或是想法比较好的问题就写一下。这道题是给定一个字母表chars和一个字符串数组,如果数组里的字符串单词可以用字母表里的字母表示出来,就认为这个单词已经掌握了,求掌握的所有单词的长度之和。
之前也做过这种有关“单词”的题目,都是需要判断一个字符串是否包含另一个字符串,刚开始做的时候是傻傻的去遍历比较,但是题目又要求每个字母只能用一次,如果有多个重复字母,又麻烦一点。对于这类问题,可以将一个字符串中每个字母的频数记录在一个长度为26的数组中,数组每一位对应一个字母,只要将字母转换为ASCII码,就可以与数组索引对应。如”zhangqingfeng”对应的频数数组为[1, 0, 0, 0, 1, 1, 3, 1, 1, 0, 0, 0, 0, 3, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1],按照这种思路求解的代码为:
class Solution {
public int countCharacters(String[] words, String chars) {
int[] count = new int[26];
int length = 0;
for(int i=0;i<chars.length();i++) count[chars.charAt(i)-97]++;
for(String s:words){
int[] tmp = new int[26];
for(int j=0;j<s.length();j++) tmp[s.charAt(j)-97]++;
boolean sign = true;
for(int k=0;k<tmp.length;k++){
if(tmp[k]>count[k]) sign = false;
}
if(sign) length += s.length();
}
return length;
}
}