Java算法笔记
- Qingfeng Zhang
- Algorithm
- November 6, 2019
Sections
1.求最大公因数-辗转相除法
两个数a,b的最大公因数等于max(a,b)-min(a,b),min(a,b)的最大公因数,依次执行直到其中一个数为0,另一个数就是a,b的最大公因数;(实际计算中为避免多次相减可以取余数)
将两个数a,b的最大公因数记为GCD(a,b),假设a,b的最大公因数为g,则有
a=m\times g, b=n\times g
其中GCD(m,n)=1,假设a>b,有:
a-b=(m-n)\times g
GCD(m-n,n)=1,a-b,b的最大公因数依然是g。
NO.914 卡牌分组
将卡牌分为任意组,每组的元素数量(不小于2)和值相同,是否存在这样的分组,需要计算所有数出现次数的最大公因数:
class Solution {
public boolean hasGroupsSizeX(int[] deck) {
Map<Integer,Integer> map = new HashMap<>();
for(int n: deck){
map.put(n,map.containsKey(n)?map.get(n)+1:1);
}
int factor = map.get(deck[0]);
for(Integer n: map.keySet()){
int num = map.get(n);
factor = comput(num,factor);
if(factor==1) return false;
}
return true;
}
public int comput(int a,int b){ //计算最大公因数
return b==0?a:comput(b,a%b);
}
}
2.计算质数-厄拉多塞筛法
要求找出2~N范围内的所有质数,可以先找到第一个质数2,然后划掉2的倍数,然后找到下一个质数3,然后划掉3的倍数,再找到下一个质数5……这很像一个筛子,将不满足的数筛掉,留下满足要求的数,这个方法叫做厄拉多塞筛法 ;
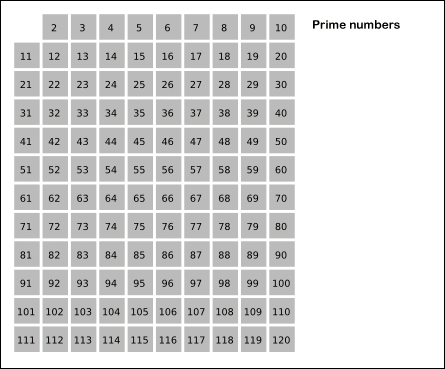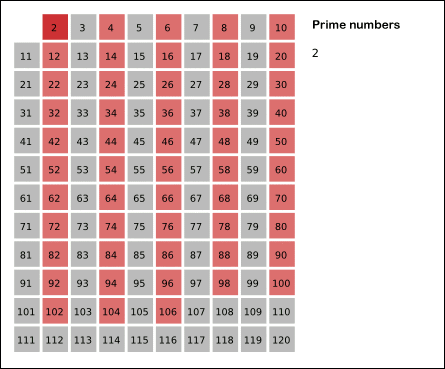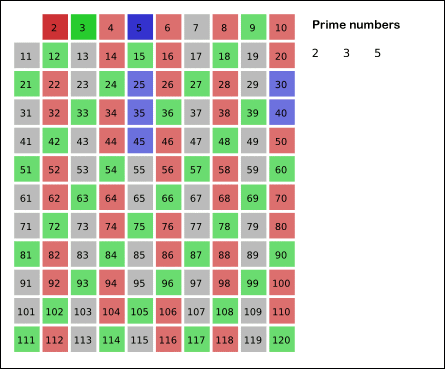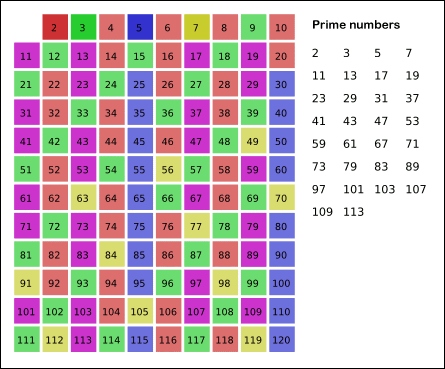
NO.204 计数质数
统计所有小于非负整数n的质数的数量:
class Solution {
public int countPrimes(int n) {
boolean[] A = new boolean[n];
int count = 0;
for(int i=2;i<Math.sqrt(n);i++){
if(!A[i]){ //下一个没有被划掉的就是质数
int k = 2; //从质数的2倍开始,也可以从i*i开始
while(i*k<n){
A[i*k] = true; //划掉质数的倍数
k++;
}
}
}
for(int i=2;i<n;i++){
if(!A[i]) count++; //统计剩下的质数数量
}
return count;
}
}
3.约瑟夫环问题
约瑟夫问题:N个人围成一圈,从第一个人开始报数,报到M的将出局,下一个人接着从1开始报数,如此反复直到最后一个人即为胜利者;
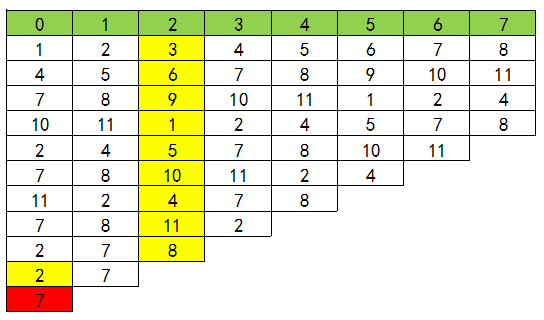
这个问题可以用环形链表模拟,但是时间复杂度较高,将N个人编号为1,2,3,…N,假设N=11,M=3,则:
第一次,1开始报数,3出局;
第二次,4开始报数,6出局;
第三次,7开始报数,9出局;
……最后的胜利者为7;
这个过程的递推公式为:
f(N,M) = (f(N-1,M)+M)%N
可以理解为每次删掉第i个人后,将第i+1个人放在第一个位置,然后开始报数,这个讲解的很好约瑟夫问题;
NO.面试题62 圆圈中最后剩下的数字
class Solution {
public int lastRemaining(int n, int m) {
//f(n,m) = (f(n-1,m)+n)%n
//其中f(n,m)表示有n个人间隔为m时最后剩下的数的坐标
int p = 0;
for(int i=2;i<=n;i++){
p = (p+m)%i;
}
return p;
}
}
4.卡特兰数Catalan
卡特兰数是组合数学中一个经常在各种计数问题中出现的数列,以一个问题为例:使用n个矩形拼成n阶梯形,问拼接的方法有多少种,如下图:

n阶梯形包含n个“尖”,每一个“尖”都恰好属于一个矩形,以n=6为例,包含尖角的矩形有以下6种:
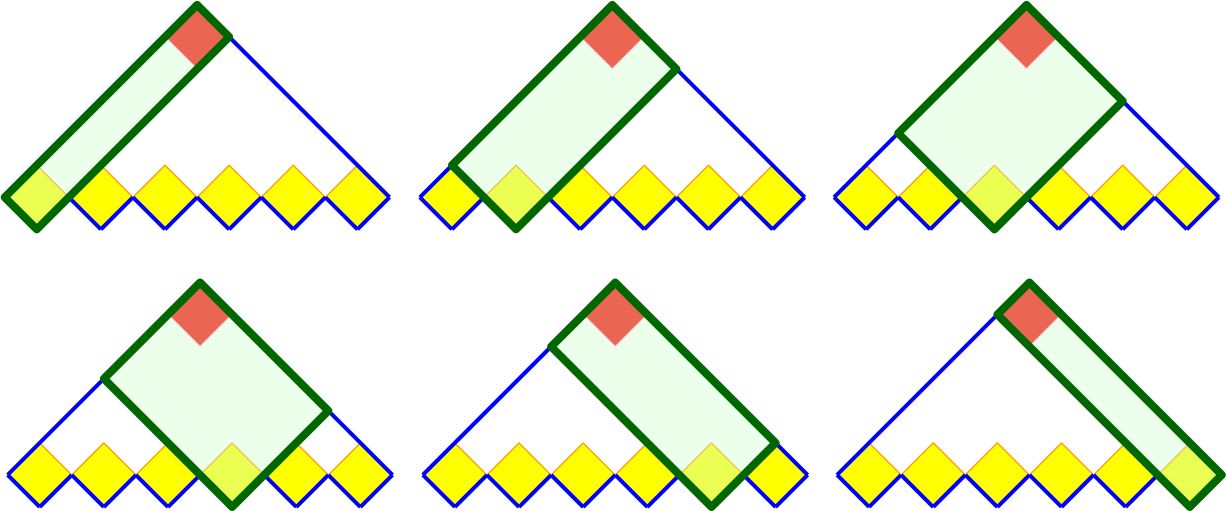
如果用 C_n 表示将n阶梯形分解为n个矩形的方法数,则由于每个尖角都可以将梯形分为左右两部分,如下:
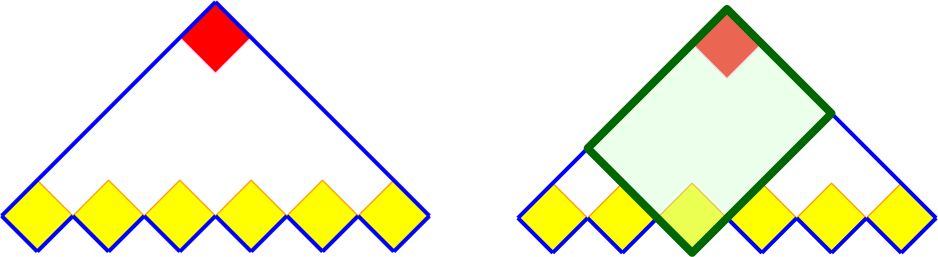
因此有:
C_6 = C_0C_5 + C_1C_4 + C_2C_3 + C_3C_2 + C_4C_1 + C_5C_0
对分解的情况进行推广可以得到 C_n 一般项公式为:
C_n = C_0C_{n-1}+C_1C_{n-2}+C_2C_{n-3}+…+C_{n-2}C_1+C_{n-1}C_0
其中n与 C_n 可以由下式表达:
C_n = \frac{1}{n+1}\dbinom{2n}{n} = \frac{1}{n+1}C_{n}^{2n} = \frac{(2n)!}{(n+1)!n!}
常见问题
1.括号匹配:
给定n个’(‘和n个’)’,要求左括号和右括号是匹配的,求可能的结果;

2.Dyck words:
给定n个’X’和n个’Y’组成字符串,要求从第一个字符开始的子串中’X’的个数不少于’Y’的个数,求可能的结果;
3.标准Yang表:
给定一个2*n的方格表,填入数字1~2n,要求每行自左而右、每列自上而下都是严格递增的,求有多少种填法;
如果令第一行的值表示’(‘的位置,第二行的值表示’)’的位置,那么这个问题和括号匹配一样;

4.不相交的弦:
在一个源上分布着2n个点,连接两点得到一天弦,共有n条弦,要求弦之间不相交,求连接的方式总数;
如果从圆上某一点开始沿着圆周,遇到某条弦的第一个点写下一个’(‘,遇到某条弦的第二个点写下一个’)’,这个问题也可以转换为括号匹配问题;

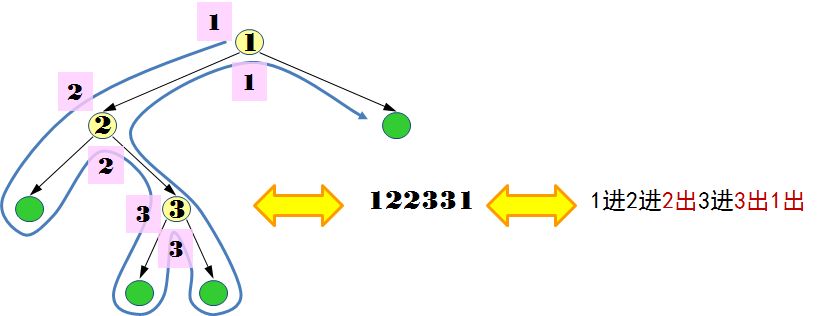
5.出栈序列:
假设入栈顺序为1,2,…,n,求所有可能的出栈序列,这其实也和括号匹配一样;
6.笔画“群峰”:
使用n个斜向上的线段和n个相同长度的斜向下的线段,画出“群峰”;如果用’(‘代替斜向上的线段,’)’代替斜向下的线段,则可以转换为括号匹配的问题;

7.满位置二叉树的计数:
有n+1个叶子节点的满位置二叉树(每个节点有0或2个子节点)的种数;
例如当n=3,有以下5种满位置二叉树:
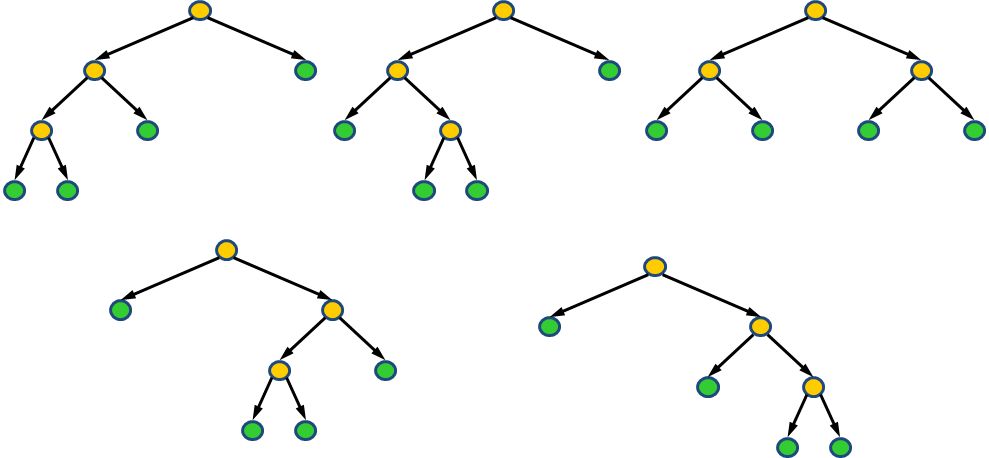
考虑树的前序遍历:第一次遇到一个非叶子节点,写下一个’(‘,第二次遇到一个非叶子节点,写下一个’)’,从而将问题转换为括号匹配;
NO.22 括号生成
class Solution {
List<String> l = new ArrayList<>();
public List<String> generateParenthesis(int n) {
dfs("",n,0,0);
return l;
}
public void dfs(String s,int n,int left,int right){
if(s.length()==2*n){
l.add(s);
return ;
}
if(left<n){
dfs(s+'(',n,left+1,right);
}
if(right<left){
dfs(s+')',n,left,right+1);
}
}
}