Java-动态规划算法
- Qingfeng Zhang
- Algorithm
- March 10, 2020
Sections
动态规划的一般形式是求最值 ,这个过程中会对问题的可能解答进行穷举,因为这类问题会存在重叠子问题 ,暴力穷举效率会非常低,所以需要DP
table 来优化穷举的过程,避免不必要的计算,此外,动态规划问题会具备最优子结构 ,因此才能由子问题的最值得到原问题的最值;
动态规划的三个要素是:重叠子问题,最优子结构,状态转移方程;
把所求的结果一步步分解称作自顶向下,而从最简单、规模最小的问题逐步求得最终解称作自底向上;
2020-3-29 关于动态规划的一些总结
最近一直在做动态规划的一些中等题,感觉智商急剧下降,经常自闭,今天做题突然有了一下感悟,就在这总结一下;
有些动态规划题会给出一个备选的数组,然后给定一个目标值,要求找出用数组中的值达到目标值的所有可能种数;
我把这类问题分为两种:给定数组中的元素不能重复使用和可以重复使用,而这两种情况对应着两种不同的解题策略:
1.遍历给定数组的每个元素,每次更新dp数组的值,从而得到计算结果 2.按索引顺序遍历dp数组,每次更新dp数组当前位置的值,从而得到计算结果
先说下0-1背包问题,0-1背包问题给定n个重量为w_1,w_2,...,w_n,价值为v_1,v_2,...,v_n的物品和一个容量为C的背包,求能装下的物品的最大价值,这个问题中就会要求每个物品只能使用一次,这里可以定义dp[i][j]为加入第i个物品且容量为j时的最大价值,也可以将dp定义为一维数组,表示容量为i时的最大价值,然后逐个放入物品然后更新dp,下面的例子中C=11,有5件物品: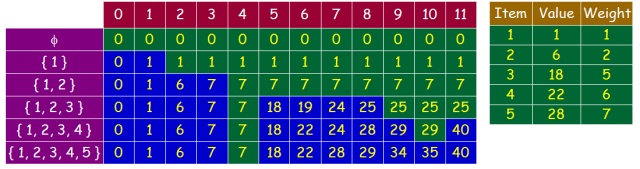
0-1背包问题中有两个状态,也就是物品i和容量c,因此需要一个两层循环遍历,每次有两种选择:将第i个物品放入背包和不放入背包。
- 如
NO.322 零钱兑换给定一个数组表示不同面额的硬币和一个总金额,求用总金额兑换的最少硬币数量,数组值可以重复使用 ; - 如
NO.377 组合总和IV给定一个无重复的数组和一个目标数,找出和为目标数的组合的个数,数组值可以重复使用 ; - 如
NO.416 分割等和子集给定一个数组,问能否将这个数组分为两个和相等的部分,其实就是判断是否有等于sum/2的组合,数组值不能重复使用 ; - 如
NO.474 一和零中给定一个字符串数组,其中每个字符都是0或1,然后给定一个目标:0的数量m和1的数量n,要求出用这m个0和n个1可以组成数组中的字符串的数量,数组值不能重复使用 ; - 如
NO.494 目标和中给定一个非负整数数组和一个目标数,对于数组中的数可以添加+或-号,求添加符号后运算的结果等于目标数的组合数量,数组值不能重复使用 ;
但是这类问题也不能一概而论,像NO.139 单词拆分也是判断能否用字符串数组中的字符串(可以重复使用)组成给定字符串,但是用动态规划加String.contains()更方便。
1.股票问题
股票问题可以用一个三维dp数组来说清楚:dp[i][k][0 or
1],表示当前为第i天且已经进行了k次交易,手上是否持有股票(1表示持有,0表示不持有)时的最大利润;
最终的最大利润即在最后一天不持有股票且用完交易次数时的利润,对于比较简单的NO.121、NO.122、NO.309,可以将这个三维的dp数组减少到二维,因为交易次数是1或是无穷,也可以用两个一维数组甚至几个变量来实现动态规划;
但是对于NO.123这种限定了交易次数的情况,就需要使用dp数组中的这个维度,因此dp数组为三维或是两个二维数组;
NO.121 买卖股票的最佳时机
给定一个数组,第i个值表示第i天的股票价格,要求只能完成一笔交易(买入和卖出),求最大的收益;
这是最基础的动态规划问题,只需要用一个变量记录第i天之前的股票最低价格min,就可以得到第i天卖出的收益prices[i]-min,记录收益的最大值就是结果:
class Solution {
public int maxProfit(int[] prices) {
int min = Integer.MAX_VALUE;
int profit = 0;
for(int i=0;i<prices.length;i++){
min = Math.min(min,prices[i]);
profit = Math.max(profit,prices[i]-min);
}
return profit;
}
}
NO.122 买卖股票的最佳时机II
又是一道经典的股票问题,与上一题不同的地方在于没有限制股票的买入卖出次数,同样要求最大的利润;
根据股票问题的动态规划解题思路,每一天都有两种状态:持有股票和不持有股票,因此可以建立两个dp数组,分别表示两种状态每一天的当前利润(也就是每个值表示当前身上的总金额),那么dp数组如何更新?
对于持有股票的dp1 ,如果在第i天持有股票,可能是第i-1天就持有股票没卖出,也可能是第i-1天不持有股票,并且在第i天买入当天的股票;同理,对于不持有股票的dp2,如果在第i天不持有股票,可能是第i-1天就不持有股票,也可能是第i-1天持有股票,并且在第i天当天卖出,因此两个dp数组的计算公式为:
dp1[i]=max(dp1[i-1],dp2[i-1]-prices[i])
dp2[i]=max(dp2[i-1],dp1[i-1]+prices[i])
(Python语法是真的简洁…)在最后一天不持有股票时的总金额就是最大利润;
class Solution {
public int maxProfit(int[] prices) {
if(prices.length<=1){
return 0;
}
int[] dp1 = new int[prices.length];
int[] dp2 = new int[prices.length];
dp1[0] = -prices[0];
dp2[0] = 0;
for(int i=1;i<prices.length;i++){
dp1[i] = dp1[i-1]>dp2[i-1]-prices[i]?dp1[i-1]:dp2[i-1]-prices[i];
dp2[i] = dp2[i-1]>dp1[i-1]+prices[i]?dp2[i-1]:dp1[i-1]+prices[i];
}
return dp2[dp2.length-1];
}
}
但是提交之后时间并不是很好,看来还有更好的解法,果不其然,贪心法才是这题的最优解法;
贪心思想就是如果价格上涨我就前一天买入,然后卖出(题目也说可以买卖同一支股票,因此可以同一天买入卖出),然后累加收益就行;
class Solution {
public int maxProfit(int[] prices) {
if(prices.length<=1){
return 0;
}
int profit = 0;
for(int i=1;i<prices.length;i++){
if(prices[i-1]<prices[i]){
profit += prices[i]-prices[i-1];
}
}
return profit;
}
}
NO.123 买卖股票的最佳时机III
与上一题的区别在于限定交易的次数为2次,上面两道题的交易次数为1和不限制,比较好做,因此这道题需要在dp数组中加上一个维度表示交易的次数;
令dp1[i][j]表示持有股票且交易j次时的利润,dp2[i][j]表示不持有股票且交易j次时的利润,因此,在遍历prices数组的时候,对于每天的股票价格,需要再计算交易次数为1,2时的最大利润,也就是多了一层循环;
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==0) return 0;
int[][] dp1 = new int[prices.length][3]; //dp1[i][j]表示持有股票且交易j次时的利润
int[][] dp2 = new int[prices.length][3]; //dp2[i][j]表示不持有股票且交易j次时的利润
dp1[0][1] = dp1[0][2] = -prices[0];
for(int i=1;i<prices.length;i++){
for(int k=1;k<=2;k++){
dp1[i][k] = Math.max(dp1[i-1][k],dp2[i-1][k-1]-prices[i]); //买入算一次交易
dp2[i][k] = Math.max(dp2[i-1][k],dp1[i-1][k]+prices[i]);
}
}
return dp2[prices.length-1][2];
}
}
可以省略为四个变量,想想!
NO.188 买卖股票的最佳时机IV
这题的交易次数有限制,但是限制次数是一个变量,因此分两种情况:如果次数达到了prices数组的一半,则相当于次数没限制,此时和NO.122一样;否则就按照NO.123的思路进行求解;
class Solution {
public int maxProfit(int k, int[] prices) {
if(prices.length==0) return 0;
if(k>=prices.length/2){ //当建议次数达到prices长度的一半,相当于没限制,与之前的股票交易问题一样
int[] dp1 = new int[prices.length];
int[] dp2 = new int[prices.length];
dp1[0] = -prices[0];
for(int i=1;i<prices.length;i++){
dp1[i] = Math.max(dp1[i-1],dp2[i-1]-prices[i]);
dp2[i] = Math.max(dp2[i-1],dp1[i-1]+prices[i]);
}
return dp2[prices.length-1];
}else{
int[][] dp1 = new int[prices.length][k+1]; //持有的dp数组
int[][] dp2 = new int[prices.length][k+1]; //不持有的dp数组
System.out.println(k);
for(int n=1;n<=k;n++){
dp1[0][n] = -prices[0];
}
for(int i=1;i<prices.length;i++){
for(int n=1;n<=k;n++){
dp1[i][n] = Math.max(dp1[i-1][n],dp2[i-1][n-1]-prices[i]); //买入算一次交易
dp2[i][n] = Math.max(dp2[i-1][n],dp1[i-1][n]+prices[i]);
}
}
return dp2[prices.length-1][k];
}
}
}
NO.309 最佳买卖股票时机含冷冻期
问题定义与一般的股票问题一样,不同之处在于这里的买卖股票包含冷冻期,即当天卖出之后第二天不能再买入(冷冻期一天);
依然是定义dp1[i]为第i天持有股票的最大收益,dp2[i]为第i天不持有股票的最大收益,对于冷冻期这个限制,只需要在更新dp1[i]的时候使用dp1[i-1],dp2[i-2]和prices[i]即可,为什么是dp2[i-2]下面给出解释:
如果没有冷冻期的话就是用dp2[i-1]没问题;对于昨天不持有股票可能是昨天卖了(dp1[i-1]+prices[1])或是没卖(dp2[i-1]),但是如果是卖了而得到最大收益,会因为有冷冻期而不考虑,即:
dp2[i] = max(dp2[i-1],dp1[i-1]+prices[i])
因为dp1[i-1]+prices[i]不被考虑,所以对于dp1[i+1]来说,dp2[i]==dp2[i],所以要取前前一天的dp2,因此得到dp1和dp2的更新公式:
dp1[i] = max(dp1[i-1],dp2[i-1]+prices[i])
dp2[i] = max(dp2[i-1],dp1[i-2]+prices[i])
class Solution {
public int maxProfit(int[] prices) {
int len = prices.length;
if(len==0) return 0;
int[] dp1 = new int[len+1];
int[] dp2 = new int[len+1];
dp1[1] = -prices[0];
for(int i=2;i<=len;i++){
dp1[i] = Math.max(dp1[i-1],dp2[i-2]-prices[i-1]);
dp2[i] = Math.max(dp2[i-1],dp1[i-1]+prices[i-1]);
}
return dp2[len];
}
}
可以使用三个变量代替两个数组,优化空间:
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==0) return 0;
int dp1 = -prices[0], dp2 = 0, pre = 0;
for(int i=1;i<prices.length;i++){
int tmp = dp2;
dp2 = Math.max(dp2,dp1+prices[i]);
dp1 = Math.max(dp1,pre-prices[i]);
pre = tmp;
}
return dp2;
}
}
2.打家劫舍
NO.198 打家劫舍
给定一个数组,数组的每个元素表示房屋内可以偷窃的金额,但是不能连续盗窃两家,否则会触发警报,求最大可偷窃的金额;
当小偷走到某一家的时候有两种选择:1.偷窃这并且前一家没有偷窃;2.不偷窃这家,说明偷窃了前一家;因此在当前位置可以获得的最大金额是这两种情况中的,可以定义一个dp数组,其中dp[i]表示在前i家可以偷窃的最大金额
,用状态转移方程表示就是:dp[i] = max(dp[i-1], dp[i-2]+nums[i])
可以将数组改为常数个变量:
class Solution {
public int rob(int[] nums) {
// if(nums.length==0) return 0;
// int[] dp = new int[nums.length+1];
// dp[1] = nums[0];
// for(int i=2;i<=nums.length;i++){
// dp[i] = Math.max(dp[i-1],dp[i-2]+nums[i-1]);
// }
// return dp[nums.length];
if(nums.length==0) return 0;
int tmp1=0, tmp2=nums[0];
for(int i=1;i<nums.length;i++){
int tmp = Math.max(tmp2,tmp1+nums[i]);
tmp1 = tmp2;
tmp2 = tmp;
}
return tmp2;
}
}
NO.213 打家劫舍II
这道题与上面的打家劫舍唯一的不同是房屋是首尾相连的,也就是不同同时偷窃第一家和最后一家;
在计算后面的最大值时,怎么知道这个最大金额有没有包括第一家的?一开始想在为每一个金额设置一个标签,表示这里的金额中是否包含第一家,然后在最后一家和倒数第二家中取最大值,但是问题是这两家的金额可能都包含第一家的啊。。。
按照题目的要求,结果有两种可能:1.没有偷窃了第一家,最后一家有没有偷窃不重要;2.没有偷窃了最后一家,有没有偷窃第一家不重要(这里的不重要是按照动态规划计算最大值,能让结果最大就行);基于此分析,可以设置两个dp数组分别表示两种情况的结果,而每种情况的计算就和上一题一样了:
class Solution {
public int rob(int[] nums) {
if(nums.length==0) return 0;
if(nums.length==1) return nums[0];
int[] dp1 = new int[nums.length+1];
int[] dp2 = new int[nums.length+1];
dp1[1] = nums[0];
for(int i=2;i<=nums.length;i++){
dp1[i] = Math.max(dp1[i-1],dp1[i-2]+nums[i-1]);
dp2[i] = Math.max(dp2[i-1],dp2[i-2]+nums[i-1]);
}
return Math.max(dp1[nums.length-1],dp2[nums.length]);
}
}
NO.337 打家劫舍III
这次偷窃的是按照树形排列的房屋,并且要求不能同时偷窃相连的两个房屋,求可以盗取的最大金额;
本来一看到打家劫舍就想到了动态规划,但是这居然是一个树的问题,又要用到DFS;但是还是用到了基本动态规划的思想,除了房屋的位置和树结构相似,其他和最基本的打家劫舍问题一样,对于当前的节点有两种选择:1.盗取当前的节点,然后放弃左右孩子节点;2.放弃当前节点,从左右孩子节点中盗取最大值,按照此思路实现的代码如下:
class Solution {
public int rob(TreeNode root) {
// 最高金额是下面的最大值:
// 1.抢劫当前节点和抢劫左右节点的子树的值;
// 2.抢劫当前节点的左右子树的值;
// 依次递归求解
if(root==null) return 0;
int val = 0;
if(root.left!=null) val += rob(root.left.left)+rob(root.left.right);
if(root.right!=null) val += rob(root.right.left)+rob(root.right.right);
return Math.max(root.val+val,rob(root.left)+rob(root.right));
}
}
上面的写法很费时,按照上面的思想,可以用长度为2的dp数组完成,dp[0]表示不抢劫当前节点所得到的最多的钱,dp[1]表示抢劫当前节点得到的最多的钱,每一个节点都有一个dp数组,最后得到根节点的dp数组就是结果:
class Solution {
public int rob(TreeNode root) {
int[] result = dp(root);
return Math.max(result[0],result[1]);
}
public int[] dp(TreeNode root){
if(root==null) return new int[2];
int[] l = dp(root.left);
int[] r = dp(root.right);
int[] tmp = new int[2]; // 当前节点的dp数组
tmp[0] = Math.max(l[0],l[1])+Math.max(r[0],r[1]); //不抢劫root的最大获益
tmp[1] = root.val+l[0]+r[0]; //抢劫root的最大获益
return tmp;
}
}
3.字符串公共子序列问题
这类问题是以求两个字符串的公共子序列为基础的,不要求公共子序列连续,但是要保证顺序不变,如:abcdef和aceg的公共子序列ace;
NO.583 两个字符串的删除操作
给定两个单词word1和word2,每次可以任意删除两个单词中的一个字母,要使得删除后两个单词相同,求最少的删除次数;
这题其实就是包装了一下的最长公共子序列,最要求出两个单词最长的公共子序列,删除次数也就确定了;
定义dp[i][j]为word1的[0,i]与word2的[0,j]的最长公共子序列,dp的更新策略为:
dp[i][j]= \begin{cases} dp[i-1][j-1]+1& \text{if word1[i]=word2[j]}\\ max(dp[i-1][j],dp[i][j-1])& \text{otherwise} \end{cases}
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length(), len2 = word2.length();
int[][] dp = new int[len1+1][len2+1];
for(int i=1;i<=len1;i++){
for(int j=1;j<=len2;j++){
if(word1.charAt(i-1)==word2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1]+1;
}else{
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return len1+len2-2*dp[len1][len2];
}
}
NO.712 两个字符串的最小ASCII删除和
给定两个字符串s1和s2,同样进行NO.583中的删除操作使得两个字符串相等,求删除的字符的ASCII值的和;
这题虽然过程和上题一样,但是所求的结果不一样,这里需要知道删去字符的ASCII值的和,因此,可以定义dp[i][j]表示使得s1的[0,i]和s2的[0,j]相等的删除字符的ASCII之和,从而写出dp的更新策略为:
dp[i][j]= \begin{cases} dp[i-1][j-1]& \text{if word1[i]=word2[j]}\\ min(dp[i-1][j]+s1[i],dp[i][j-1]+s2[j],dp[i-1][j-1]+s1[i]+s2[j])& \text{otherwise} \end{cases}
class Solution {
public int minimumDeleteSum(String s1, String s2) {
int sum = 0;
int len1 = s1.length(), len2 = s2.length();
int[][] dp = new int[len1+1][len2+1];
for(int i=1;i<=len1;i++){
dp[i][0] = dp[i-1][0]+(int)s1.charAt(i-1);
}
for(int j=1;j<=len2;j++){
dp[0][j] = dp[0][j-1]+(int)s2.charAt(j-1);
}
for(int i=1;i<=len1;i++){
for(int j=1;j<=len2;j++){
if(s1.charAt(i-1)==s2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = Math.min(dp[i-1][j-1]+(int)s1.charAt(i-1)+(int)s2.charAt(j-1),Math.min(dp[i-1][j]+(int)s1.charAt(i-1),dp[i][j-1]+(int)s2.charAt(j-1)));
}
}
}
return dp[len1][len2];
}
}
NO.1035 不相交的线
给定两个数组表示两条平行线,数组值表示线上点的坐标,可以将两条水平线上的点进行相连,但是每条线不能相交,求线的最大数量;
这题乍一看不好做,但是者其实只是包装的比较好而已,剥掉外壳会发现这和NO.583一模一样,也是求最长公共子序列;
class Solution {
public int maxUncrossedLines(int[] A, int[] B) {
int len1 = A.length, len2 = B.length;
int[][] dp = new int[len1+1][len2+1];
for(int i=1;i<=len1;i++){
for(int j=1;j<=len2;j++){
if(A[i-1]==B[j-1]){
dp[i][j] = dp[i-1][j-1]+1;
}else{
dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
}
}
}
return dp[len1][len2];
}
}
NO.72 编辑距离
题目一般是按题号升序,但是这是道困难题,所以就放这里了;
给定两个单词word1和word2,可以对任意一个单词进行三种操作:插入一个字符、删除一个字符、替换一个字符,结果还是使得两个单词相等,求最少的操作次数;
这题和NO.583很像,但是NO.583只能删除,这里还可以插入和替换,似乎不好办,但是可以参照NO.712的思路,重新定义dp数组,这里按照题意定义dp[i][j]为使得word1的[0,i]和word2[0,j]相等的最少操作次数,从而写出dp的更新策略为:
dp[i][j]= \begin{cases} dp[i-1][j-1]& \text{if word1[i]=word2[j]}\\ min(dp[i-1][j],dp[i][j-1],dp[i-1][j-1])+1& \text{otherwise} \end{cases}
class Solution {
public int minDistance(String word1, String word2) {
int len1 = word1.length(), len2 = word2.length();
int[][] dp = new int[len1+1][len2+1];
for(int i=1;i<=len1;i++){
dp[i][0] = i;
}
for(int j=1;j<=len2;j++){
dp[0][j] = j;
}
for(int i=1;i<=len1;i++){
for(int j=1;j<=len2;j++){
if(word1.charAt(i-1)==word2.charAt(j-1)){
dp[i][j] = dp[i-1][j-1];
}else{
dp[i][j] = Math.min(dp[i-1][j-1],Math.min(dp[i][j-1],dp[i-1][j]))+1;
}
}
}
return dp[len1][len2];
}
}
其他的动态规划问题
NO.91 解码方法
给定一个数字组成的字符串,通过'A'->1,'B'->2,...,'Z'->26对字符串进行解码,求解码方法的总数;
看一个例子:[1,2,2]有三种解码:
1 - 2 - 2
12 - 2
1 - 22
加入一个新元素2之后有3+2种解码:
1 - 2 - 2 - ‘2’
12 - 2 - ‘2’
1 - 22 - ‘2’
(新增加的结果:)
‘1’ - ‘2’ - ‘22’
‘12’ - ‘22’
前面三种是直接将2单独放在每种解码的后面,后面两种是将2与每种解码最后的值合并(如果合法的话),此题也即是考虑这些情况:
定义dp[i]是nums前i个字符可以得到的解码种数,假设之前的字符串是abcx,现在新加入了y,则有以下5种情况:
1.如果x==’0’,且y==’0’,无法解码,返回0;
2.如果只有x==’0’,则y只能单独放在最后,不能与x合并(不能以0开头),此时有:
dp[i] = dp[i-1]
3.如果只有y==’0’,则y不能单独放置,必须与x合并,并且如果合并结果大于26,返回0,否则有:
dp[i] = dp[i-2]
4.如果 xy<=26:
则y可以“单独”放在abcx的每个解码结果之后后,并且如果abcx以x单独结尾,此时可以合并xy作为结尾,而这种解码种数就是abc的解码结果,此时有:
dp[i+1] = dp[i] + dp[i-1]
5.如果 xy>26: 此时x又不能与y合并,y只能单独放在dp[i]的每一种情况的最后,此时有:
dp[i+1] = dp[i]
class Solution {
public int numDecodings(String s) {
char[] arr = s.toCharArray();
int[] dp = new int[s.length()+1];
dp[0] = 1;
dp[1] = arr[0]=='0'?0:1;
if(s.length()<=1) return dp[1];
for(int i=2;i<=s.length();i++){
int n = (arr[i-2]-'0')*10+(arr[i-1]-'0');
if(arr[i-1]=='0' && arr[i-2]=='0'){
return 0;
}else if(arr[i-2]=='0'){
dp[i] = dp[i-1];
}else if(arr[i-1]=='0'){
if(n>26) return 0;
dp[i] = dp[i-2];
}else if(n>26){
dp[i] = dp[i-1];
}else{
dp[i] = dp[i-1]+dp[i-2];
}
}
return dp[dp.length-1];
}
}
NO.120 三角形的最小路径和
给定一个二维list,记作triangle,第i行包含i个元素,呈现一个三角形的结构,将从第一层走到最后一层经过的值的和算作路径长,求最短路径,每次只能走到左下或是右下的位置;
一看到这种问题,当然先想到动态规划,先建立一个二维数组,数组每个位置表示从第一层到这里的最短路径,问题不就迎刃而解了吗,下面是求解的代码:
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int h = triangle.size();
int w = triangle.get(triangle.size()-1).size();
int[][] dp = new int[h][w];
dp[0][0] = triangle.get(0).get(0);
for(int i=1;i<h;i++){
for(int j=0;j<triangle.get(i).size();j++){
int tmp = triangle.get(i).get(j);
if(j==0){dp[i][j] = tmp+dp[i-1][j];}
else if(j==triangle.get(i).size()-1){
dp[i][j] = tmp+dp[i-1][j-1];
}else{
dp[i][j] = tmp+Math.min(dp[i-1][j-1],dp[i-1][j]);
}
}
}
int min = Integer.MAX_VALUE;
for(int n:dp[h-1]){min = Math.min(n,min);}
return min;
}
}
这里可以做一个改进:将自顶向下的遍历改为自底向上的遍历;因为每个三角形的每个位置都有左下角和右下角(除了最后一行),但是不一定都有左上角和右上角,自底向上的遍历省去了一些边界情况,还有就是第一行只有一个元素,遍历到顶的结果就是最终结果,而遍历到底的结果还要求最小值;
问题可以这么简单地做,但是题目又提出了一个进阶的要求:使用一维的数组;按行遍历三角形的时候一维数组怎么保存结果?每次都要用dp的值来计算并更新dp数组,这不就冲突了吗,其实仔细想想发现并没有,当在遍历三角形的第k行时,dp保存的是从最后一层到第k+1行每个位置的最短路径长,更新dp[i]会用到dp[i]和dp[i+1]以及triangle[k][i],但是注意:更新完dp[i]后,后面计算dp[i+1]与dp[i]无关,因此可以在使用dp的同时更新dp,代码如下:
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
int[] dp = new int[triangle.size()+1]; //把dp初始化为长度为triangle.size()+1的全0数组;
for(int i=triangle.size()-1;i>=0;i--){
for(int j=0;j<triangle.get(i).size();j++){
dp[j] = Math.min(dp[j],dp[j+1])+triangle.get(i).get(j);
}
}
return dp[0];
}
}
NO.174 地下城游戏
题目简单来说就是,给定一个数组,每个值表示到达当前位置需要消耗的生命值或是补充的生命值,当生命值小于等于0则死亡,求从数组的左上角走到右下角所需要的最小初始生命值;
这道题其实一看就知道是动态规划,但是好像又没那么简单,所以因为要求的是一条路径中的最小累加和,所以还用了两个数组来记录,最终越做越复杂。。。
其实这题的关键在于从右下角往左上角遍历
,而dp[i][j]就表示从位置(i,j)到达右下角所需的最小生命值,最终算到dp[0][0],而转移方程就是:
dp[i,j] = max(1,min(dp[i+1][j],dp[i][j+1])-dungeon[i][j])
因为就算路径上全是正数,也需要初始生命值为1;
class Solution {
public int calculateMinimumHP(int[][] dungeon) {
//dp[i][j]表示到达dungeon[i][j]所需的最小生命值
int h = dungeon.length, w = dungeon[0].length;
int[][] dp = new int[h][w];
dp[h-1][w-1] = dungeon[h-1][w-1]>0?1:1-dungeon[h-1][w-1];
for(int i=h-2;i>=0;i--){
dp[i][w-1] = Math.max(1,dp[i+1][w-1]-dungeon[i][w-1]);
}
for(int j=w-2;j>=0;j--){
dp[h-1][j] = Math.max(1,dp[h-1][j+1]-dungeon[h-1][j]);
}
for(int i=h-2;i>=0;i--){
for(int j=w-2;j>=0;j--){
dp[i][j] = Math.max(1,Math.min(dp[i+1][j],dp[i][j+1])-dungeon[i][j]);
}
}
return dp[0][0];
}
}
NO.221 最大正方形
给定一个包含0和1二维矩阵,求出其中由1组成的最大正方形的面积;
做过很多这样的01矩阵问题,有的是把1当作岛屿,求岛屿面积,有的是求每个1到最近的0的距离……这类问题很多是用DFS或BFS,而这题是求正方形的面积,DFS不可行,而可以由小正方形面积求出大正方形的面积,因此用动态规划求解;
定义dp[i][j]是以matrix[i][j]作为右下角的最大正方形的边长长度则:
if dp[i][j]==0 dp[i][j] = 0
if dp[i][j]==1 && matrix[i-k][j]>0 && matrix[i-k][j]>0; k=1,2,…,dp[i-1][i-2]:
dp[i][j] = dp[i-1][j-1]+1
else:
dp[i][j] = 1
这样的话对于就要遍历求边长,如:
\begin{matrix} 1 & 1 & 1 & 0 \\ 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \\ 1 & 0 & 1 & 1 \end{matrix}
在计算dp[3][3]的时候要看第4行和第4列是否全为1,否则边长缩短,求解的代码如下:
class Solution {
public int maximalSquare(char[][] matrix) {
if(matrix.length==0) return 0;
int result = 0;
int[][] dp = new int[matrix.length][matrix[0].length];
for(int i=0;i<matrix.length;i++){
dp[i][0] = matrix[i][0]-'0';
result = Math.max(result,dp[i][0]);
}
for(int j=0;j<matrix[0].length;j++){
dp[0][j] = matrix[0][j]-'0';
result = Math.max(result,dp[0][j]);
}
for(int i=1;i<matrix.length;i++){
for(int j=1;j<matrix[0].length;j++){
if(matrix[i][j]!='1') continue;
int len = 0;
for(int x=1;x<=dp[i-1][j-1];x++){
if(dp[i-x][j]>0 && dp[i][j-x]>0){
len++;
}else{break;}
}
dp[i][j] = len+1;
result = Math.max(result,dp[i][j]);
}
}
return result*result;
}
}
可以对方法进行改进,dp依旧使用上面的定义,但是更新dp[i][j]时候不用遍历寻找最大边长,而是取左上角、左边、上面的均填充为1的最大面积:
dp[i][j] = Min(dp[i-1][j-1],dp[i-1][j],dp[i][j-1])
求解的代码如下:
class Solution {
public int maximalSquare(char[][] matrix) {
if(matrix.length==0) return 0;
int result = 0;
int h = matrix.length, w = matrix[0].length;
int[][] dp = new int[h+1][w+1];
for(int i=1;i<=h;i++){
for(int j=1;j<=w;j++){
if(matrix[i-1][j-1]=='0') continue;
dp[i][j] = 1+Math.min(dp[i-1][j-1],Math.min(dp[i-1][j],dp[i][j-1]));
result = Math.max(result,dp[i][j]);
}
}
return result*result;
}
}
NO.264 丑数II
丑数是因数里只包含2,3,5的正整数,认为1也是丑数,求第n个丑数;
第一眼看到就觉得这是一个一般的动态规划问题,dp[i]可以由dp[i/2],dp[i/3],dp[i/5]求得(如果可以整除),但是如果用数组,事先又不知道数组长度,因为有非丑数,如果用ArrayList或HashSet又会超时,难办。。。
有一个很妙但是又感觉很普通(为什么自己没有想到)的方法:三指针,使用三个指针,每次取三个指针分别乘以2,3,5中的最小结果,即是下一个丑数,然后将取得最小结果的指针后移一位,感觉像是上面的想法倒过来实现,只是每次要保证得到的是最小的丑数:
class Solution {
public int nthUglyNumber(int n) {
// if(n==1) return 1;
// int count = 1, i = 2;
// int[] factor = {2,3,5};
// List<Integer> l = new ArrayList<>();
// l.add(1);
// l.add(1);
// while(count<n){
// l.add(0);
// for(int num: factor){
// if(i>=num && i%num==0 && l.get(i/num)==1){
// l.set(l.size()-1,1);
// count++;
// break;
// }
// }
// i++;
// }
// return l.size()-1;
int a=0, b=0, c=0;
int[] arr = new int[n];
arr[0] = 1;
for(int i=1;i<n;i++){
int ugly = Math.min(arr[a]*2,Math.min(arr[b]*3,arr[c]*5));
arr[i] = ugly;
if(arr[i]==arr[a]*2) a++;
if(arr[i]==arr[b]*3) b++;
if(arr[i]==arr[c]*5) c++;
}
return arr[n-1];
}
}
NO.300 最长上升子序列
给定一个无序的整数数组,找出其中最长的上升子序列的长度,上升子序列不要求连续;
动态规划:定义dp[i]表示前i个值可以组成的最长上升序列的长度,然后求dp[i+1]的时候用k遍历前面i个dp值,取nums[k]<nums[i+1]中dp[k]的最大值再加1,时间复杂度是O(n^2):
class Solution {
public int lengthOfLIS(int[] nums) {
if(nums.length<=1) return nums.length;
int max = 0;
int[] dp = new int[nums.length];
dp[0] = 1;
for(int i=1;i<nums.length;i++){
dp[i] = 1;
for(int j=i-1;j>=0;j--){
if(nums[j]<nums[i]){
dp[i] = Math.max(dp[i],dp[j]+1);
}
}
max = Math.max(max,dp[i]);
}
return max;
}
}
还有一个更好的方法:贪心算法+二分查找;上面的方法可以使用二分查找改善时间复杂度因为tmp是递增的,因此可以使用二分查找得到所插入的位置:
class Solution {
public int lengthOfLIS(int[] nums) {
if(nums.length<=1) return nums.length;
int[] tmp = new int[nums.length];
tmp[0] = nums[0];
int len = 0;
for(int n: nums){
int l=0, r=len;
while(l<r){
int m = (l+r)/2;
if(tmp[m]>=n){
r = m;
}else{l = m+1;}
}
tmp[l] = n;
if(l==len) len++;
}
return len;
}
}
NO.322 零钱兑换
给定一些不同面额的硬币coins和一个总金额amount,将总金额兑换成数量最少的硬币,如果不能兑换返回-1;
用动态规划求解的话就很简单,但前提是想得到,先建立一个dp数组保存之前计算的结果,定义dp[i]为金额为i时兑换零钱的最小数量,由此,对于每一个面额c的零钱有:dp[i] = dp[i-c]+1, if dp[i-c]!=-1
基于以上的分析,只需要从头遍历dp数组,同时修改dp[i]为兑换零钱的最小数量,最终dp[amount]就是答案:
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount+1];
for(int i=1;i<=amount;i++){
int min = Integer.MAX_VALUE;
for(int c: coins){
if(i>=c && dp[i-c]!=-1){
min = Math.min(min,dp[i-c]+1);
}
}
dp[i] = min!=Integer.MAX_VALUE?min:-1;
}
return dp[amount];
}
}
NO.368 最大整除子集
非常眼熟但是没做出来的题,给定一个数组,找出其最大的子数组且该子数组满足:任意的两个元素a,b有a%b==0或b%a==0;
一开始而没想到用什么方法就又想用DFS,结果又是超时,迫于无奈看了大佬的解法,感觉自己真的变傻了。第一个问题
在于自己把a%b==0或b%a==0想的太复杂,为什么要拿两个数来试这两个条件?如果a>b>0,只可能a%b==0,b%a一定不是0,所以只要对数组排序,使其从小到大排列,然后直接用后面的数除前面的数就行;第二个问题
是以为每加入一个数都要和原数组中每个数都判断一下,但是如果a>b>c,a%b==0,b%c==0,不就有a%c==0吗;
因此可以定义dp[i]表示nums前i个数可以组成的最大整除子集的大小,在计算dp[i]的时候,遍历nums的0~i-1为j,如果nums[i]%nums[j]==0,则表示可以在dp[j]的最大整除子集中加入nums[i],即dp[i]=dp[j]+1,在遍历过程中取dp[i]的最大值:
class Solution {
public List<Integer> largestDivisibleSubset(int[] nums){
List<Integer> result = new ArrayList<>();
if(nums.length==0) return result;
Arrays.sort(nums);
int[] dp = new int[nums.length];
Arrays.fill(dp,1);
int p = 0, max = 1;
for(int i=1;i<dp.length;i++){
for(int j=0;j<i;j++){
if(nums[i]%nums[j]==0){
dp[i] = Math.max(dp[i],dp[j]+1);
if(dp[i]>max){
max = dp[i];
p = i;
}
}
}
}
for(int k=p;k>=0;k--){
if(nums[p]%nums[k]==0 && dp[k]==max){
result.add(nums[k]);
max--;
}
}
return result;
}
}
NO.375 猜数字得大小II
给定一个正整数n,可以从1n之间任选一个数,另一个人来猜这个数,如果猜的是x且猜错则需要支付金额为x的现金,猜对所选的数则赢得游戏,问题要求的是至少有多少金额才能保证赢得游戏?j中确保赢得最小金额,则对于任意x在i~j中,有dp[i][j]
= min(max(dp[i][x-1],dp[x+1][j])+x),重点是先更新dp[i][i+1] ,再更新dp[i][i+2]
…最后就可以得到结果dp[0][n];
一开始以为每次取二分是最好的选择,但是错了,比如:1,2,3,4,5,每次猜二分的结果则最大金额为7,但其实可以先猜2,再猜4,这样只要有金额为6就可以保证获胜;
接着想到了动态规划,我每次选倒数第四个i-4,如果小了的话就直接猜倒数第二个i-2,如果大了,i-4前面的结果就是dp[i-5],这里的倒数第四个可以递推为7,15,31…但是这样做可以正确得到125之前的结果,后面就错了,不知道为啥;
其实自己只想到了一般,i-4前的结果是dp[i-5],那i-4之后的结果不就是dp[i-3]吗,但是怎么更新前后的dp值,这里就需要一个二维dp数组,定义dp[i][j]表示在i
class Solution {
public int getMoneyAmount(int n) {
int[][] dp = new int[n+1][n+1];
for(int k=1;k<n;k++){
for(int i=1;i+k<=n;i++){
int min = Integer.MAX_VALUE;
for(int x=i;x<i+k;x++){
min = Math.min(min,Math.max(dp[i][x-1],dp[x+1][i+k])+x);
}
dp[i][i+k] = min;
}
}
return dp[1][n];
}
}
NO.376 摆动序列
连续数字之间的差严格在正负之间交替的序列称为摆动序列,给定一个数组,求摆动序列的最大长度,可以不要求序列连续,但是要保持原始顺序;
一开始的想法是遍历每次比较三个数:x,y,z,tmp指向x,如果这三个数是摆动序列,则更新tmp为y,否则不更新,然后y,z向后遍历,每次更新摆动序列长度加1,但是长度的初始值1还是2有点麻烦,最后结果也超过了100%;
大佬的解法太妙了,有点像股票问题的做法,用up记录nums前面上升的最大长度,用down记录nums前面下降的最大长度,然后遍历过程中交替更行up和down;
class Solution {
public int wiggleMaxLength(int[] nums) {
// if(nums.length<=1) return nums.length;
// if(nums.length==2) return nums[0]==nums[1]?1:2;
// int tmp = nums[0];
// int len = nums[0]==nums[1]?1:2;
// for(int i=2;i<nums.length;i++){
// if(nums[i]!=tmp) len = Math.max(len,2);
// if((nums[i-1]-tmp)*(nums[i]-nums[i-1])<0){
// len++;
// tmp = nums[i-1];
// }
// }
// return len;
if(nums.length==0) return 0;
int up = 1, down = 1;
for(int i=1;i<nums.length;i++){
if(nums[i]>nums[i-1]) up = down+1;
if(nums[i]<nums[i-1]) down = up+1;
}
return Math.max(up,down);
}
}
NO.416 分割等和子集
给定一个只包含正整数的数组,是否可以将数组分为两部分,两部分的和相等;
首先可以用DFS来做,其次也可以用动态规划,一开始的错误思路是想令dp[i]表示nums中是否有和为i的组合,这没有问题但是更新的思路有问题,如果遍历dp数组,然后更新每一位,那dp[i]怎么计算?看dp[i-num]是否为true?这是可以重复使用nums中每个元素的情况,因为dp[i-num]中可能已经包含了num;
这里换换思路,不是遍历dp更新每一位,而是遍历nums,每次更新dp
,也就是每次加入一个num,然后记录dp中哪些和是可以得到的,可以定义dp[nums.length][target],也可以定义为一维数组:
class Solution {
public boolean canPartition(int[] nums) {
// int sum = 0;
// for(int n: nums) sum += n;
// if(sum%2!=0) return false;
// for(int n: nums){
// if(n>sum/2) return false;
// if(n==sum/2) return true;
// }
// Arrays.sort(nums);
// return dfs(nums,sum/2,nums.length-1);
// }
// public boolean dfs(int[] nums,int target,int i){
// boolean sign = false;
// if(i>nums.length || target<0) return false;
// if(target==0) return true;
// for(int k=i;k>=0;k--){
// sign = sign || dfs(nums,target-nums[k],k-1);
// }
// return sign;
// }
int sum = 0;
for(int n: nums) sum += n;
if(sum%2!=0) return false;
int target = sum/2;
boolean[] dp = new boolean[target+1];
dp[0] = true;
for(int n: nums){
for(int i=target;i>=0;i--){
if(n==i || (i-n>=0 && dp[i-n])){
dp[i] = true;
}
}
}
return dp[target];
}
}
NO.474 一和零
给定一个字符串数组和最大的0和1的个数m,n,数组中每个字符串只包含0和1,求用m个0和n个1可以组成数组中最多几个字符串(不重复);
令dp[i][j]表示用i个0和j个1可以组成的字符串数量,遍历字符串数组,每加入一个字符串更新一次dp数组,最后的结果就是dp[m][n];
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
int[][] dp = new int[m+1][n+1];
for(int i=0;i<strs.length;i++){
int a = 0, b = 0;
for(char c: strs[i].toCharArray()){
if(c=='0'){a++;}
else{b++;}
}
for(int j=m;j>=a;j--){
for(int k=n;k>=b;k--){
dp[j][k] = Math.max(dp[j][k],dp[j-a][k-b]+1);
}
}
}
return dp[m][n];
}
}
NO.494 目标和
给定一个数组nums和一个目标数S,可以对数组中的每个数进行加或减,如果可以得到结果为目标数则是一个符合要求的方法,求方法的总数;
首先这道题可以用暴力枚举来做,列出所有的情况,也就是回溯法,但是这样比较耗时;
使用动态规划来求解,定义dp数组的dp[i][j]表示nums的前i个数可以组成结果为j的方法数,而这个结果j是在[-sum,sum]内,sum是数组nums的和,因此dp数组的维度是[nums.length][sum*2+1],最后得到的dp[nums.length-1]就是对nums中所有数进行加减可能得到的所有结果及其方法数:
class Solution {
public int findTargetSumWays(int[] nums, int S) {
int sum = 0, result = 0;
for(int n: nums) sum += n;
if(sum<S) return 0;
int[][] dp = new int[nums.length][sum*2+1];
dp[0][sum-nums[0]]++;
dp[0][sum+nums[0]]++;
for(int i=1;i<nums.length;i++){
for(int j=0;j<sum*2+1;j++){
if(j-nums[i]>=0){
dp[i][j] += dp[i-1][j-nums[i]];
}
if(j+nums[i]<sum*2+1){
dp[i][j] += dp[i-1][j+nums[i]];
}
}
}
return dp[nums.length-1][S+sum];
}
}
NO.518 零钱兑换II
给定一个数组coins表示不同面值的硬币,可以重复使用,计算面额amount可以兑换硬币的方式,不同顺序的兑换看作同一种;
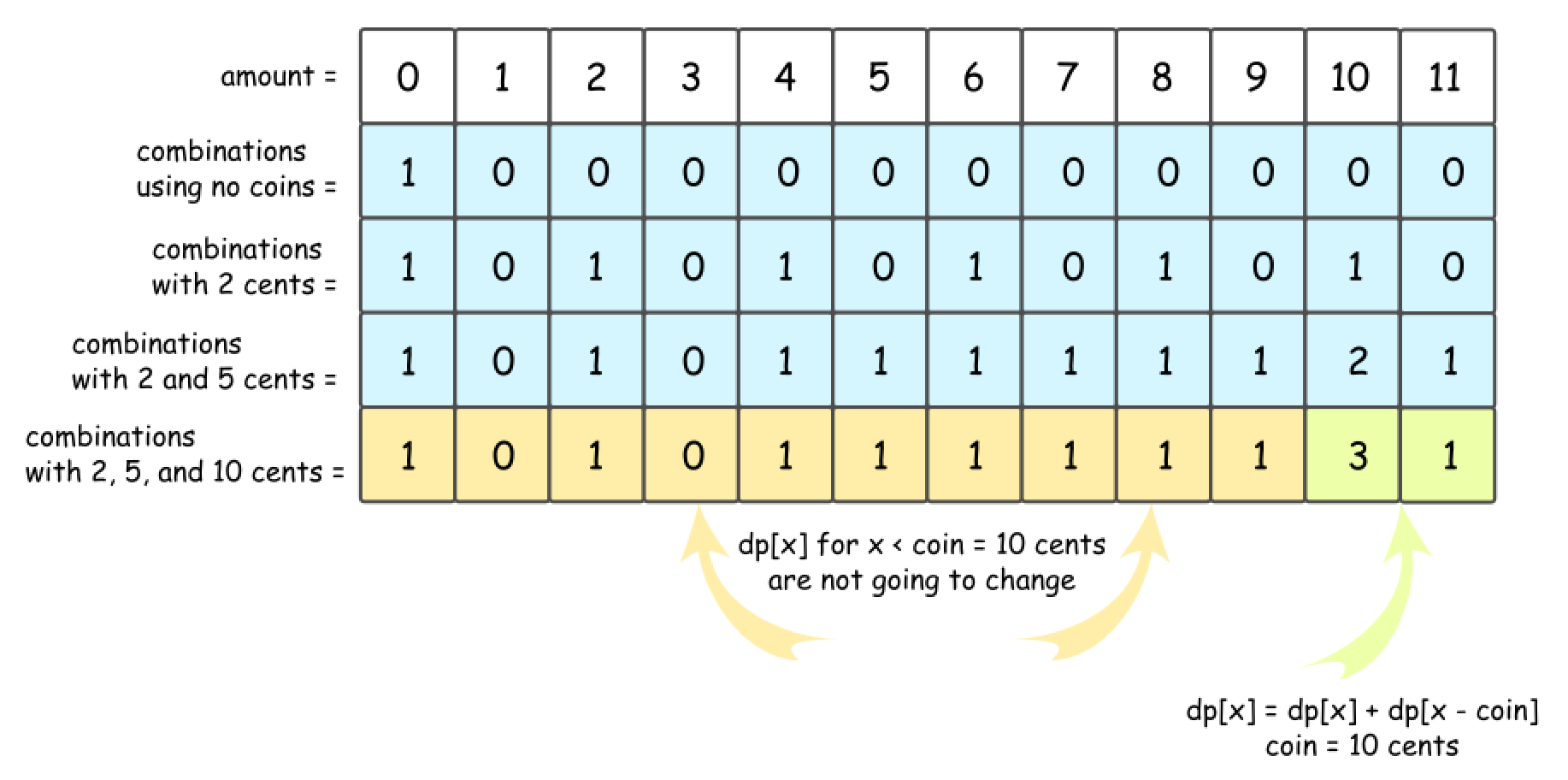
之前零钱兑换的问题只需要计算最少的硬币数量,这里要求所有的兑换方式,可以定义dp[i][j]表示面额为i时使用前j种硬币兑换的方式数,计算方式可以看作每加入一种硬币j计算一次在前j种硬币下dp[i]种每种金额的兑换种数,即:
dp[i] = dp[i]+dp[i-coin]
class Solution {
public int change(int amount, int[] coins) {
int[] dp = new int[amount+1];
dp[0] = 1;
for(int coin: coins){
for(int i=coin;i<=amount;i++){
dp[i] += dp[i-coin];
}
}
return dp[amount];
}
}
NO.576 出界的路径数
给出一个矩阵的大小,一个最大步数,一个位置坐标,从这个坐标开始,每次可以向上下左右走一步,走出矩阵边界则是一条出界路径,求所有的出界路径数;
又是一道DFS解出来超时再用动态规划求解的题目,定义在第k步时的dp[i][j]是从位置[i,j]走出界的路径数,因此每一步都会有一个dp矩阵,且有:
第k+1步中,dp[i][j]为上下左右四个方向的路径数的和,如果[i,j]的下一步出界,则路径数加1:
class Solution {
public int findPaths(int m, int n, int N, int i, int j) {
if(N==0) return 0;
int mod = 1000000007;
int[][] direct = {{1,0},{-1,0},{0,1},{0,-1}};
int[][] dp = new int[m][n];
for(int k=0;k<N;k++){
int[][] tmp = new int[m][n];
for(int x=0;x<m;x++){
for(int y=0;y<n;y++){
for(int[] d: direct){
if(x+d[0]<0 || x+d[0]>=m || y+d[1]<0 || y+d[1]>=n){
tmp[x][y]++;
}else{
tmp[x][y] = (tmp[x][y]+dp[x+d[0]][y+d[1]])%mod;
}
}
}
}
dp = tmp;
}
return dp[i][j];
}
}
NO.718 最长重复数组问题
题目非常容易理解,给定两个数组,找出其中最长的公共数组,要求公共数组是连续的,一开始看到这道题的时候没有想到用dp的方法,但是也没有想到其他什么方法。。。
以两个数组为例:A=[1,2,3,2,1],B=[3,2,1,4,7],可以使用一个dp数组来保存每次计算的结果,dp[i][j]表示数组A[:i]和B[:j]的最长公共数组的长度,注意这里的公共数组要求是以A[i]和B[j]结尾,因此当A[i]!=B[j]时,令dp[i][j]=0,如果A[i]==B[j],令dp[i][j]=dp[i-1][j-1]+1,最终只要找到dp数组中的最大值就是结果;
可以将dp数组的维度加1以省略初始化的步骤,但是要注意一下索引值:
class Solution {
public int findLength(int[] A, int[] B) {
int[][] dp = new int[A.length+1][B.length+1];
int result = 0;
for(int i=1;i<=A.length;i++){
for(int j=1;j<=B.length;j++){
if(A[i-1]==B[j-1]){
dp[i][j] = dp[i-1][j-1]+1;
result = Math.max(result,dp[i][j]);
}
}
}
return result;
}
}