Java-BFS与DFS

Sections

一直感觉DFS和回溯法没什么区别，其实它们意思很相近，回溯法是把问题分步解决，在每一步都尝试所有的可能，当找到结果或是当前方式不对时，就退回到上一步，这个过程一般会递归实现。当把回溯法用于树时，就是深度优先搜索(DFS)，几乎同义。
不管是用Java还是Python，回溯算法的基本解题思想还是一样的：可以把问题的解转化成图或树的结构表示，然后用深度优先遍历进行搜索，期间会进行剪枝处理以减少时间消耗 ，就是语法方面会有一点不同。一般会定义一个函数用于递归，递归有两种选择：选择当前的数或是不选，前一种是往深度方向探索，后一种是回溯到当前节点的下一个节点（就是图的深度优先遍历啊，在纸上画一画就明白了）。

1.组合总数问题

NO.39 组合总数

题目给定一个数组nums和一个目标值target，找出nums中和为target的所有组合，每个组合长度无限制，但不能重复，这个题目一看就是要用回溯法来做，在一棵树上从根节点开始生长，如果存在一个节点，从根节点到该节点的路径和为target，则该条路径就是一个组合。

class Solution {  
    public List<List<Integer>> combinationSum(int[] candidates, int target) {  
        List<List<Integer>> result = new ArrayList<>();  
        Arrays.sort(candidates);  
        backtrack(candidates,result,target,0,0,new ArrayList<>());  
        return result;  
    }  
    public void backtrack(int[] candidates,List<List<Integer>> result,int target,int i,int sum,List<Integer> L){  
        if(i>candidates.length-1 || sum>target){return ;}  
        if(sum==target){  
            result.add(new ArrayList<>(L));  //一定要add(new ArrayList<>(L))，不能是add(L)  
            return ;  
        }  
    
        // 两种回溯的写法：  
        // 写法一：  
        // for(int start=i;start<candidates.length;start++){  
        //     if(sum>target) break;  
        //     L.add(candidates[start]);  
        //     backtrack(candidates,result,target,start,sum+candidates[start],L);  
        //     L.remove(L.size()-1);  
        // }  
    
        // 写法二：更慢一点  
        backtrack(candidates,result,target,i+1,sum,L);  
        L.add(candidates[i]);  
        backtrack(candidates,result,target,i,sum+candidates[i],L);  
        L.remove(L.size()-1);  //前面添加的值要在后面删掉，Python直接在参数里添加  
    }  
}

上面的代码中将combinationSum()函数的result变量作为参数传给无返回值的函数backtrack()，经backtrack修改，然后在combinationSum()中return result，这里backtrack()里对result添加子列表为什么是result.add(new ArrayList<>(L))，而不能是result.add(L)，Java基础不行的就不懂了吧，说的就是我自己。。。

NO.40 组合总数II

和NO.39非常像，只是这里要求元素不能重复使用；

class Solution {  
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {  
        List<List<Integer>> result = new ArrayList<>();  
        Arrays.sort(candidates);  
        backtrack(candidates,result,target,0,new ArrayList<>(),0);  
        return result;  
    }  
    public void backtrack(int[] candidates,List<List<Integer>> result,int target,int i,List<Integer> L,int sum){  
        if(sum==target){  
            if(!result.contains(L)){result.add(new ArrayList<>(L));}  
            return ;  
        }  
        if(i>candidates.length-1 || sum>target){return ;}  //放后面避免i>candidates.length-1时sum==target，因为递归传入的是i+1  
    
        // 写法一：  
        for(int start=i;start<candidates.length;start++){  
            if(candidates[start]>target) break;  //提前剪枝  
            L.add(candidates[start]);  
            backtrack(candidates,result,target,start+1,L,sum+candidates[start]);  //这里的start+1是与上一题的区别  
            L.remove(L.size()-1);  
        }  
    
        // 写法二：  
        // backtrack(candidates,result,target,i+1,L,sum);  
        // L.add(candidates[i]);  
        // backtrack(candidates,result,target,i+1,L,sum+candidates[i]);  
        // L.remove(L.size()-1);  
    }  
}

NO.216 组合总数III

要求在1~9内找不重复的k个数和为n，返回所有结果的列表，还是一个普通的回溯问题

class Solution {  
    public List<List<Integer>> combinationSum3(int k, int n) {  
        List<List<Integer>> result = new ArrayList<>();  
        backtrack(result,k,n,1,0,new ArrayList<>());  
        return result;  
    }  
    public void backtrack(List<List<Integer>> result,int k,int n, int i, int sum, List<Integer> l){  
        if(l.size()>k){return ;}  
        if(sum==n && l.size()==k){  
            result.add(new ArrayList<>(l));  
            return ;  
        }  
        for(int start=i;start<10;start++){  
            if(sum+start>n){continue;}  
            l.add(start);  
            backtrack(result,k,n,start+1,sum+start,l);  
            l.remove(l.size()-1);  
        }  
    }  
}

NO.377 组合总数IV

给定一个数组nums和一个目标数target，找出nums中和为target的组合的总数，nums中的数可以重复使用，且顺序不同为不同的组合，如[1,1,2]和[1,2,1];
正好借这道题来记录一下关于DFS，记忆化搜索，动态规划 的东西；
首先拿到这道题依旧是没有好的思路，所以依然是用DFS来试试：

class Solution {  
    int count = 0;  
    public int combinationSum4(int[] nums, int target) {  
        dfs(nums,target,0);  
        return count;  
    }  
    public void dfs(int[] nums,int res,int i){  
        if(res<0) return ;  
        if(res==0){  
            count++;  
            return ;  
        }  
        for(int k=i;k<nums.length;k++){  
            dfs(nums,res-nums[k],0);  
        }  
    }  
}

思路没有问题，但是搜索会超时，如对于nums=[1,2,3],target=35，存在35个1的组合；
虽然思路没有问题，但是上面的代码写的也不好，只是套用一下DFS的框架，可以改一下代码如下：

class Solution {  
    public int combinationSum4(int[] nums, int target) {  
        if(target==0) return 1;  
        int count = 0;  
        for(int num: nums){  
            if(target>=num){  
                count += combinationSum4(nums,target-num);  
            }  
        }  
        return count;  
    }  
}

依然有DFS的思想，但是代码简洁清晰；最基本的思想就是target的组合总数等于target-num（num是nums中任一数）的组合总数之和 ，这是本题的解题思路；
虽然上面改了一下代码，但是和一开始没多大区别，依然超时，其实仔细想想就会发现，如果我要求target的组合总数，需要知道target- num的组合总数，而要想知道target-num的组合总数，就又要求target-num-num的组合总数。。。这就是上面的暴力递归；
但是在我求target的组合总数时候，之前可能就已经把target- num的结果求出来过，那我可不可以把这些结果记录下来，在求target组合总数的时候直接使用这些结果，这就是记忆化搜索的思想 ,这里可以使用一个数组record，record[i]保存计算出的i的组合总数，这样可以省去很多重复计算：

class Solution {  
    public int combinationSum4(int[] nums, int target) {  
        int[] record = new int[target+1];  
        Arrays.fill(record,-1);  
        record[0] = 1;  
        return dfs(nums,target,record);  
    }  
    public int dfs(int[] nums,int res,int[] record){  
        int count = 0;  
        if(record[res]!=-1) return record[res];  //res的结果之前已经计算出，直接返回  
        for(int num: nums){  
            if(res>=num){  
                count += dfs(nums,res-num,record);  
            }  
        }  
        record[res] = count;  //第一次需要记录和返回，下次再遇到res可以直接得到结果  
        return count;  
    }  
}

记忆化搜索中的把前面计算的结果保存下来便于之后计算的使用是不是很耳熟，这就是动态规划的思想，动态规划就是把结果保存在dp数组中，因此这题也可以用动态规划来做：

class Solution {  
    public int combinationSum4(int[] nums, int target) {  
        int[] dp = new int[target+1];  
        dp[0] = 1;  
        for(int i=1;i<dp.length;i++){  
            for(int num: nums){  
                if(i>=num) dp[i] += dp[i-num];  
            }  
        }  
        return dp[target];  
    }  
}

综上，对于此问题，暴力DFS或递归一般不是好的解法，可以在搜索过程中加入记忆化搜索，如果能直接用动态规划做出来就最好了。

2.图的拓扑排序

简单来说，图的拓扑排序就是在一个有向图中，对所有的节点进行排序，要求排列的顺序满足有向图中的指向，拓扑排序的结果一般不止一种；

NO.210 课程表II

有n门课0~n-1需要学习，有的课程在学习之前会有先修课程，如：学完课程a之后才能学习课程b，表示为[b,a]，课程课程总数numCourses和一些先修课程的要求prerequisites，返回任意一种符合要求的课程学习顺序；
课程之间的先修关系可以看成是一个有向图，只需要求这个图的一个拓扑排序结果就行，可以使用BFS，但是有的课程可能是独立存在的，因此，图可能不会保证所有节点都相连，对于这种情况，先将所有入度为0的节点入队，对于每一个出队的节点，记录该节点并且遍历该节点的下一个节点列表，对下一个节点的入度减1，当节点的入度为0将该节点入队；
使用BFS构造拓扑排序的过程一般为：
1.初始化图中节点的入度数组和邻接表；
2.将入度为0的节点入队；
3.对队列进行BFS遍历；

class Solution {  
    public int[] findOrder(int numCourses, int[][] prerequisites) {  
        //NO.207的升级版，可以看作一个有向图，但是会有一些节点单独存在，不与图相连  
        int[] degree = new int[numCourses];  //节点的入度数组  
        List<List<Integer>> graph = new ArrayList<>();  //节点的邻接表  
        for(int i=0;i<numCourses;i++) graph.add(new ArrayList<>());  
        //入度数组和邻接表的初始化  
        for(int[] l: prerequisites){  
            degree[l[0]]++;  //l[1] --> l[0]  
            graph.get(l[1]).add(l[0]);  
        }  
        Queue<Integer> q = new LinkedList<>();  
        //将所有入度为0的节点入队  
        for(int i=0;i<numCourses;i++){  
            if(degree[i]==0) q.offer(i);  
        }  
        int[] res = new int[numCourses];  
        int p = 0;  
        while(!q.isEmpty()){  
            int tmp = q.poll();  
            res[p++] = tmp;  
            for(int n: graph.get(tmp)){  //出队节点的下一个节点入度减1  
                degree[n]--;  
                if(degree[n]==0) q.offer(n);  //入度为0的节点入队  
            }  
        }  
        if(p!=numCourses) return new int[0];  
        return res;  
    }  
}

3.八皇后等问题

八皇后问题是一个标准的回溯求解的问题，每次在棋盘上放置一个皇后时需要考虑棋盘中其它皇后的位置，如果当前没有位置可以放置，则退回到上一步重新放置……与此类似的还有数独问题；

NO.37 解数独

数独游戏是在一个9 _9的矩阵中，要求每个数都在1~9中，且每一行、每一列、每个3 3的方块(一共9个方块)中没有重复的数字，求一个数独游戏的解；
可以使用通过维持三个boolean数组来判断当前位置可以放置的数字，row[i][j]表示第i行中数字j+1已经放过了，col[i][j]表示第i列中数字j+1已经放过了，block[i][j]表示第i个块中数字j+1已经放过了；
_关于本题的总结：

1.如果将数组中的位置按照从左到右从上到下编号n=0~80，对于每一个编号可以得到其坐标[n/9,n%9];
2.同样的方式通过坐标[i,j]计算数组的分块1~9: i/3*3+j/3;
3.可以用row[i,j]=true表示第i行中j已经出现过，同理可以使用数组col、block表示每列和每个块，当想要在board[i][j]上填写数字时，三个数组中对应行列块都为false的数才能填写;

    class Solution {  
        public void solveSudoku(char[][] board) {  
            boolean[][] row = new boolean[9][9];  
            boolean[][] col = new boolean[9][9];  
            boolean[][] block = new boolean[9][9];  
            for(int i=0;i<9;i++){  
                for(int j=0;j<9;j++){  
                    if(Character.isDigit(board[i][j])){  
                        row[i][board[i][j]-'1'] = true;  
                        col[j][board[i][j]-'1'] = true;  
                        block[i/3*3+j/3][board[i][j]-'1'] = true;  
                    }  
                }  
            }  
            dfs(board,row,col,block,0);  
        }  
        public boolean dfs(char[][] board,boolean[][] row,boolean[][] col,boolean[][] block,int n){  
            if(n==81) return true;  
            int i = n/9, j = n%9;  
            if(board[i][j]!='.') return dfs(board,row,col,block,n+1);  
            for(int k=0;k<9;k++){  
                if(row[i][k] || col[j][k] || block[i/3*3+j/3][k]) continue;  
                board[i][j] = (char)(k+'1');  
                row[i][k] = col[j][k] = block[i/3*3+j/3][k] = true;  
                if(dfs(board,row,col,block,n+1)) return true;  
                row[i][k] = col[j][k] = block[i/3*3+j/3][k] = false;  
            }  
            board[i][j] = '.';  
            return false;  
        }  
    }

NO.51 N皇后

在一个N*N的棋盘上放置皇后，要求每行、每列、以该位置为中心的对角线上都只有一个皇后，求所有可能的放置结果；
乍看本题和解数独有点相似，但是解数独需要找数组中所有的空位置进行填写，所有位置的计算很巧妙，但N皇后每行每列都只有一个皇后，因此可以从第一行开始放置，则每一行都有N个位置可以放置(其中有些位置不合法)，这就是选择列表：

class Solution {  
    List<List<String>> res = new ArrayList<>();  
    public List<List<String>> solveNQueens(int n) {  
            
        boolean[] col = new boolean[n];  
        char[][] arr = new char[n][n];  
        for(int i=0;i<n;i++) Arrays.fill(arr[i],'.');  
        backtrack(arr,col,n,0);  
        return res;  
    }  
    //col[i]表示第i列已经有一个Q了，r表示第r行  
    public void backtrack(char[][] arr,boolean[] col,int n,int r){  
        if(r>=n){  //到达最后一行表示递归结束  
            List<String> l = new ArrayList<>();  
            for(char[] c: arr) l.add(String.valueOf(c));  
            res.add(l);  
            return ;  
        }  
        for(int k=0;k<n;k++){  //当前的选择列表，即在一行中选择位置填Q  
            boolean sign = false;  
            if(col[k]) continue;   //如果该列已经有Q  
            for(int a=r-1,b=k-1;a>=0&&b>=0;a--,b--){  //检查对角线是否有Q  
                if(arr[a][b]=='Q'){  
                    sign = true;  
                    break;  
                }  
            }  
            if(sign) continue;  
            for(int a=r-1,b=k+1;a>=0&&b<n;a--,b++){  //检查对角线是否有Q  
                if(arr[a][b]=='Q'){  
                    sign = true;  
                    break;  
                }  
            }  
            if(sign) continue;  
            arr[r][k] = 'Q';    
            col[k] = true;  
            backtrack(arr,col,n,r+1);  
            arr[r][k] = '.';  
            col[k] = false;  
        }  
    }  
}

其他的DFS与回溯问题

有些问题中会给出一个二维数组，比如只包含0和1，然后说明这个数组的含义，比如岛屿和海洋，这类问题一般是用DFS或BFS在矩阵中进行搜索，一般搜索会有4个或8个方向，每次搜索的下一步也是如此；
DFS是深度优先遍历，是一种思想和工具，而回溯算法是对DFS的实现，是DFS的一种应用；

NO.17 电话号码的字母组合

给定一个数字字符串（2-9），每个数字在手机九宫格键盘上都对应3或4个字母，求这个数字字符串可以对应的所有字母字符串的组合，如”23”的结果是[“ad”,”ae”,”af”,”bd”,”be”,”bf”,”cd”,”ce”,”cf”];
其实这道题容易想到是用回溯法，如果用树表示，则每一层是一个数字对应的所有字母，相互之间进行组合，但是由于水平太低不知道怎么实现：

class Solution {  
    public List<String> letterCombinations(String digits) {  
        Map<String,String> map = new HashMap<>(){{  
            put("2","abc");  
            put("3","def");  
            put("4","ghi");  
            put("5","jkl");  
            put("6","mno");  
            put("7","pqrs");  
            put("8","tuv");  
            put("9","wxyz");  
        }};  
        List<String> l = new ArrayList<>();  
        if(digits.length()==0) return l;  
        backtrack(map,l, "", digits);  
        return l;  
    }  
    public void backtrack(Map<String,String> map, List<String> l, String result, String next_digits){  
        if(next_digits.length()==0){  
            l.add(result);  
        }else{  
            String s = next_digits.substring(0,1);  //s是剩余digits的第一个字符(串)  
            String letters = map.get(s);  //letters是s在键盘上对应的字母字符串  
            for(int i=0;i<letters.length();i++){  //遍历letters  
                String letter = map.get(s).substring(i,i+1);  //letter是letters的第i个字符(串)  
                backtrack(map,l,result+letter,next_digits.substring(1));  //将result加上letter，next_digits去掉首字母  
            }  
        }  
    }  
}

看了答案还是有点懵，还需要多体会一下。

NO.78 子集

给定一个数组nums，找出nums的所有不重复子集（包含空集），首先想到的方法就是回溯，这也可以看作一个非常基本的回溯问题；

class Solution {  
    public List<List<Integer>> subsets(int[] nums) {  
        List<List<Integer>> result = new ArrayList<>();  
        Arrays.sort(nums);  
        backtrack(nums,result,0,new ArrayList<>());  
        return result;  
    }  
    public void backtrack(int[] nums,List<List<Integer>> result,int i,List<Integer> l){  
        if(i>nums.length){return ;}  
        if(!result.contains(l)){  
            result.add(new ArrayList<>(l));  //这里不能加return，因为不能终止递归；  
        }  
        //这里的循环可以理解为从一个节点产生所有分支，然后递归到第一个分支。。。  
        for(int start=i;start<nums.length;start++){  
            l.add(nums[start]);  
            backtrack(nums,result,start+1,l);  
            l.remove(l.size()-1);  
        }  
    }  
}

这里的回溯部分就用for循环的方式写了，其实for循环很容易和回溯的思想联系起来，一开始从根节点进行分支，然后在第一个子节点进行分支，由此进行深度优先遍历。
提交之后发现回溯解法比较耗时，也就是还有更好的解法，根据评论区大佬的提示，可以先用空列表初始化一个二维列表，然后对于nums中的每个元素，遍历一遍二维列表，将每个一维列表添加nums的元素，并作为新列表添加到二维列表；

class Solution {  
    public List<List<Integer>> subsets(int[] nums) {  
        List<List<Integer>> result = new ArrayList<>();  
        result.add(new ArrayList<>());  
        for(int n:nums){  
            int len = result.size();  //这里的result.size()不能写在循环里  
            for(int i=0;i<len;i++){  
                List<Integer> l = new ArrayList<>(result.get(i));  
                l.add(n);  
                result.add(l);  
            }  
        }  
        return result;  
    }  
}

NO.79 单词搜索

给定一个字母矩阵和一个单词，找出这个单词能否由矩阵的一条路径构成，不能重复使用字母；这也是回溯法的思想，对于当前的位置，需要判断其上下左右(如果存在)的字母的值，但是根据之前的框架又很难写出代码，所以这个求解代码就好好感悟一下吧！

class Solution {  
    public boolean exist(char[][] board, String word) {  
        int[][] dir = new int[][]{{0,1},{1,0},{0,-1},{-1,0}};  
        for(int i=0;i<board.length;i++){  
            for(int j=0;j<board[0].length;j++){  
                if(board[i][j]==word.charAt(0)){  
                    if(backtrack(board,word,i,j,0)){  
                        return true;  
                    }  
                }  
            }  
        }  
        return false;  
    }  
    public boolean backtrack(char[][] board,String word,int i,int j,int len){  
        if(len>=word.length()) return true;  
        if(i<0 || i>=board.length || j<0 || j>=board[0].length || board[i][j]!=word.charAt(len)){  
            return false;  
        }  
        board[i][j] -= 26;  
        boolean sign = backtrack(board,word,i+1,j,len+1) || backtrack(board,word,i-1,j,len+1) || backtrack(board,word,i,j+1,len+1) || backtrack(board,word,i,j-1,len+1);  
        board[i][j] += 26;  
        return sign;  
    }  
}

这里的backtrack函数是返回一个布尔变量，所以每次递归调用的时候都需要接收其返回值；

NO.93 复原IP地址

IP地址分为四部分，用.隔开，最大长度是12，最小长度是4，给定一个字符串，可以在字符串中添加符号.，求所有可能组成的IP地址，如给定s=”25525511135”，结果为[“255.255.11.135”, “255.255.111.35”]；
其实这道题很容易想到用回溯法，但是实现起来又是一个问题，我想到的是从一个空字符串开始，每次可以添加s的一个字符，或是添加.，停止条件：当.的数量达到3以上，停止回溯，当s遍历结束，停止回溯（判断）；
判断得到的ip是否合法可以用另外一个函数judge，将ip按.分割，如果部分字符串的长度大于3，或是转换成整数后不在0到255内，返回false，否则返回true；
（太菜了，题解没看懂，就贴上自己写的方法）

class Solution {  
    public List<String> restoreIpAddresses(String s) {  
        List<String> result = new ArrayList<>();  
        if(s.length()>12 || s.length()<4) return result;  
        backtrack(result, s, s.substring(0,1), 0, 1);  
        return result;  
    }  
    
    public void backtrack(List<String> result, String s ,String tmp, int count, int i){  
        if(count>3) return ;  
        if(i>=s.length() || tmp.length()-3==s.length()){  
            System.out.println(tmp);  
            if(count==3 && judge(tmp)){  
                result.add(tmp);  
            }  
            return ;  
        }  
        tmp = tmp+"."+s.substring(i,i+1);  
        backtrack(result,s,tmp,count+1,i+1);  
        tmp = tmp.substring(0,tmp.length()-2);  
            
        tmp = tmp+s.substring(i,i+1);  
        backtrack(result,s,tmp,count,i+1);  
        tmp = tmp.substring(0,tmp.length()-1);  
    }  
        
    public boolean judge(String ip){  
        for(String s: ip.split("\\.")){  
            if(s.length()>1 && s.charAt(0)=='0' || s.length()>3){  
                return false;  
            }  
            int n = Integer.parseInt(s);  
            if(0>n || n>255){  
                return false;  
            }  
        }  
        return true;  
    }  
}

NO.131 分割回文串

将给定的字符串为分割回文子串，要求返回所有的分割结果；
一开始没有想通，还是以为每次增加一个字符，这样就想错了，因该是判断当前的一个子串是否是回文串，如果是就添加到结果列表里面，子串的截取是从上一个回文子串的末尾开始的；

class Solution {  
    List<List<String>> res = new ArrayList<>();  
    public List<List<String>> partition(String s) {  
        dfs(s,0,new ArrayList<>());  
        return res;  
    }  
    public void dfs(String s,int i,List<String> l){  
        if(i>s.length()) return ;  
        if(i==s.length()){  
            res.add(new ArrayList<>(l));  
            return ;  
        }  
        for(int k=i;k<s.length();k++){  
            if(!judge(s,i,k)) continue;  
            l.add(s.substring(i,k+1));  
            dfs(s,k+1,l);  
            l.remove(l.size()-1);  
        }  
    }  
    public boolean judge(String s,int l,int r){  
        while(l<r){  
            if(s.charAt(l++)!=s.charAt(r--)) return false;  
        }  
        return true;  
    }  
}

NO.200 岛屿数量

同样是给定一个01矩阵，其中1表示陆地，相连的陆地为一块岛屿，这道题不是求岛屿的面积，而是求岛屿的数量；
这里主要记录一下关于这类求数量的DFS问题，一般是遍历矩阵，遇到1则从这个位置开始DFS遍历，将遍历过的位置置为0，这样一次遍历就“消灭”一块岛屿，使用一个变量计数可以得到岛屿的数量：

class Solution {  
    int[][] direct = {{0,1},{0,-1},{1,0},{-1,0}};  
    public int numIslands(char[][] grid) {  
        if(grid.length==0) return 0;  
        int h=grid.length, w=grid[0].length;  
        int count = 0;  
        for(int i=0;i<h;i++){  
            for(int j=0;j<w;j++){  
                if(grid[i][j]=='1'){  
                    dfs(grid, i, j);  
                    count++;  
                }  
            }  
        }  
        return count;  
    }  
    public void dfs(char[][] grid, int i, int j){  
        int h=grid.length, w=grid[0].length;  
        if(i<0 || i>=h || j<0 || j>=w || grid[i][j]!='1'){  
            return ;  
        }  
        grid[i][j] = '0';  
        dfs(grid, i+1, j);  
        dfs(grid, i-1, j);  
        dfs(grid, i, j+1);  
        dfs(grid, i, j-1);  
    }  
}

NO.322 零钱兑换

给定一些不同面额的硬币coins和一个总金额amount，将总金额兑换成数量最少的硬币，如果不能兑换返回-1；
这题很容易想到使用回溯法，因为大不了将所有的兑换结果都求出来，然后再记录数量最少的结果，但是这样做超时了；
当然，兑换是从最大面额的硬币开始兑换，但是很容易出现一种面额的硬币重复兑换很多次，如果每次都要递归的话就很耗时了，因此可以计算出可以兑换的一种硬币最大数量，同时注意剪枝，将结果明显大于当前最小数量的结果略掉：

    class Solution {  
        int result = Integer.MAX_VALUE;  
        public int coinChange(int[] coins, int amount) {  
            Arrays.sort(coins);  
            backtrack(coins,coins.length-1,amount,0);  
            return result==Integer.MAX_VALUE?-1:result;  
        }  
        public void backtrack(int[] coins,int i, int res, int count){  
            if(res==0){  
                result = Math.min(result,count);  
                return ;  
            }  
            if(i<0 || res<0) return ;  
            int k = res/coins[i];  
            for(int start=k;start>=0;start--){  
                if(count+start>result) break;  
                System.out.println(start);  
                backtrack(coins,i-1,res-start*coins[i],count+start);  
            }  
        }  
    }

最后的for循环其实没有很明白；

NO.337 打家劫舍III

这次偷窃的是按照树形排列的房屋，并且要求不能同时偷窃相连的两个房屋，求可以盗取的最大金额；
本来一看到打家劫舍就想到了动态规划，但是这居然是一个树的问题，又要用到DFS；对于当前的节点有两种选择：1.盗取当前的节点，然后放弃左右孩子节点；2.放弃当前节点，从左右孩子节点中盗取最大值，按照此思路实现的代码如下：

class Solution {  
    public int rob(TreeNode root) {  
        // 最高金额是下面的最大值：  
        // 1.抢劫当前节点和抢劫左右节点的子树的值；  
        // 2.抢劫当前节点的左右子树的值；  
        // 依次递归求解  
            if(root==null) return 0;  
            int val = 0;  
            if(root.left!=null) val += rob(root.left.left)+rob(root.left.right);  
            if(root.right!=null) val += rob(root.right.left)+rob(root.right.right);  
            return Math.max(root.val+val,rob(root.left)+rob(root.right));  
        }  
}

上面的写法很费时，按照上面的思想，可以用长度为2的dp数组完成,dp[0]表示不抢劫当前节点所得到的最多的钱，dp[1]表示抢劫当前节点得到的最多的钱，每一个节点都有一个dp数组，最后得到根节点的dp数组就是结果：

class Solution {  
    public int rob(TreeNode root) {  
        int[] result = dp(root);  
        return Math.max(result[0],result[1]);  
    }  
    public int[] dp(TreeNode root){  
        if(root==null) return new int[2];  
        int[] l = dp(root.left);  
        int[] r = dp(root.right);  
        int[] tmp = new int[2];  // 当前节点的dp数组  
        tmp[0] = Math.max(l[0],l[1])+Math.max(r[0],r[1]);  //不抢劫root的最大获益  
        tmp[1] = root.val+l[0]+r[0];  //抢劫root的最大获益  
        return tmp;  
    }  
}

NO.417 太平洋大西洋水流问题

给定一个矩阵表示一片大陆上每个位置的高度，太平洋位于左边界和上边界，大西洋位于右边界和下边界，规定水流只能按照上下左右四个方向流动，并且不能向高度更高的地方流动，要求找到所有既可以流到太平洋又可以流到大西洋的坐标；
这道题乍一看给出的是一个矩阵，其实就可以想到是用DFS，一开始是想遍历矩阵，对每一个位置都进行DFS，如果该位置可以流到太平洋和大西洋，就记录坐标，看起来想法很简单，但是实际写代码还要考虑其他问题：DFS中如何记录已经遍历过的位置，如何同时判断可以流到太平洋和大西洋……当然可以硬着头皮写，这样的结果就是费时费力，而且结果不优，因此做题不能只靠主观想法，可能想法很简单，但是实际实现不容易，还要想想策略；
这道题有一个非常巧妙地想法：逆流，即不考虑从当前位置能否同时流到两个大洋，而是考虑从两个大洋可以逆流到大陆中地哪些位置，并且使用两个矩阵，一个表示太平洋可以逆流流到的位置，另一个表示大西洋可以逆流流到的位置，并且可以将逆流流到的位置的值置为true，从而记录DFS中已经遍历的位置防止重复遍历，最后将两个矩阵中同时为true的位置坐标保存即是结果；

class Solution {  
    int[][] direct = {{0,1},{0,-1},{1,0},{-1,0}};  
    public List<List<Integer>> pacificAtlantic(int[][] matrix) {  
        List<List<Integer>> result = new ArrayList<>();  
        if(matrix.length==0) return result;  
        int h=matrix.length, w=matrix[0].length;  
        boolean[][] Pacific = new boolean[h][w];  
        boolean[][] Atlantic = new boolean[h][w];  
        for(int i=0;i<h;i++){  
            dfs(matrix,i,0,Pacific,matrix[i][0]);  
            dfs(matrix,i,w-1,Atlantic,matrix[i][w-1]);  
        }  
        for(int j=0;j<w;j++){  
            dfs(matrix,0,j,Pacific,matrix[0][j]);  
            dfs(matrix,h-1,j,Atlantic,matrix[h-1][j]);              
        }  
        for(int m=0;m<h;m++){  
            for(int n=0;n<w;n++){  
                if(Pacific[m][n] && Atlantic[m][n]){  
                    List<Integer> l = Arrays.asList(m,n);  
                    result.add(l);  
                }  
            }  
        }  
        return result;  
    }  
    public void dfs(int[][] matrix,int i,int j,boolean[][] record,int pre){  
        if(i<0 || i>=matrix.length || j< 0 || j>=matrix[0].length || record[i][j] || matrix[i][j]<pre){  
            return ;  
        }  
        record[i][j] = true;  
        for(int[] d: direct){  
            dfs(matrix,i+d[0],j+d[1],record,matrix[i][j]);  
        }  
    }  
}

NO.473 火柴拼正方向

给定一个数组，其中每个数字表示火柴的长度，判断用所有的火柴能不能拼成一个正方形；
题目的意思非常简单，但是一开始并没有想到用DFS怎么做，其实可以把问题看作往四条边上放火柴，正方形的边长是可以算出来的，如果有一条边的长度大于边长，则这个情况就不符合，所以还是遍历所有情况，然后找出符合要求的：

class Solution {  
    public boolean makesquare(int[] nums) {  
        int sum = 0;  
        for(int n: nums) sum += n;  
        if(sum%4!=0 || nums.length<4) return false;  
        Arrays.sort(nums);  
        return dfs(nums,nums.length-1,0,0,0,0,sum/4);  
    }  
    public boolean dfs(int[] nums,int i,int l1,int l2,int l3,int l4,int len){  
        if(l1>len || l2>len || l3>len || l4>len) return false;  
        if(l1==len && l2==len && l3==len && l4==len){  
            return true;  
        }  
        return dfs(nums,i-1,l1+nums[i],l2,l3,l4,len) || dfs(nums,i-1,l1,l2+nums[i],l3,l4,len) || dfs(nums,i-1,l1,l2,l3+nums[i],l4,len) || dfs(nums,i-1,l1,l2,l3,l4+nums[i],len);  
    }  
}

这种题目是遍历所有情况，只要其中有一种符合要求，就可以得到最终的结果，而有的题目是需要在所有情况中找出符合要求的多种结果；
换个角度可以把这个问题看成用四个容量相等的桶接水的问题，解题思路和上面一样，换个写法如下：

class Solution {  
    public boolean makesquare(int[] nums) {  
        int sum = 0;  
        for(int n: nums) sum += n;  
        if(sum%4!=0 || nums.length<4) return false;  
        Arrays.sort(nums);  
        return judge(nums,nums.length-1,new int[4],sum/4);  
    }  
    public boolean judge(int[] nums,int i,int[] edge,int len){  
        if(i<0){  
            if(edge[0]==len && edge[1]==len && edge[2]==len && edge[3]==len){  
                return true;  
            }  
        }  
        for(int k=0;k<4;k++){  
            if(edge[k]<len && edge[k]+nums[i]<=len){  
                edge[k] += nums[i];  
                if(judge(nums,i-1,edge,len)) return true;  
                edge[k] -= nums[i];  //用第k个桶接水只是一种尝试，需要还原；  
            }  
        }  
        return false;  
    }  
}

NO.542 01矩阵

给定一个矩阵包含0和1，计算矩阵中每个位置距离最近的0的距离；
这题一开始也是想着用DFS，如果当前位置的值不为0，取当前位置四个方向各个位置“距0最短距离”的最小值加1，这因该是最直观的想法，应该是可行的，但是结果里总有几个位置的值计算错了，没想明白；
其实这题可以用点小技巧，使用广度优先遍历BFS ，先将矩阵中为0的位置入队，为1的位置置为MAX_VALUE（表示这些值需要修改）；每次出队一个位置，计算该位置周围四个方向的值：如果小于等于中间值则不用修改，如果大于中间值则等于中间值加1，并将该位置入队（根据该位置修改的结果再修改周围四个方向的值）：

class Solution {  
    public int[][] updateMatrix(int[][] matrix) {  
        int[][] direct = {{1,0},{-1,0},{0,1},{0,-1}};  
        Queue<int[]> q = new LinkedList<>();  
        for(int i=0;i<matrix.length;i++){  
            for(int j=0;j<matrix[0].length;j++){  
                if(matrix[i][j]==0){  
                    q.offer(new int[]{i,j});  
                }else{  
                    matrix[i][j] = Integer.MAX_VALUE;  
                }  
            }  
        }  
        while(!q.isEmpty()){  
            int[] tmp = q.poll();  
            for(int[] d: direct){  
                int x=tmp[0]+d[0], y=tmp[1]+d[1];  
                if(x>=0 && x<matrix.length && y>=0 && y<matrix[0].length){  
                    if(matrix[x][y]>matrix[tmp[0]][tmp[1]]+1){  
                        matrix[x][y] = matrix[tmp[0]][tmp[1]]+1;  
                        q.offer(new int[]{x,y});  
                    }  
                }  
            }  
        }  
        return matrix;  
    }  
}

感悟就是不要一看到这种搜索有关的题就只想到用DFS，偶尔也要想想用BFS能不能做（BFS一般通过队列实现），和这样非常相似的NO.1162 地图分析这道题。

NO.547 朋友圈

还是给定一个二维01数组，但是这里的含义不一样，[i,j]表示第i个人和第j个人是朋友，因此属于一个朋友圈，求朋友圈的数量，一开始看到感觉和岛屿数量类似，但是岛屿是向四个方向遍历，而这里有点像图的邻接矩阵，第i行中为1的列都是i的朋友，由此得到：

class Solution {  
    Set<Integer> set = new HashSet<>();  
    public int findCircleNum(int[][] M) {  
        int count = 0;  
        for(int i=0;i<M.length;i++){  
            for(int j=0;j<M[0].length;j++){  
                if(j>i && M[i][j]==1){  
                    search(M,i,j);  
                    count++;  
                }  
            }  
        }  
        if(set.size()<M.length){  
            count += M.length-set.size();  
        }  
        return count;  
    }  
    public void search(int[][] M,int i,int j){  
        Queue<int[]> q = new LinkedList<>();  
        for(int n=i+1;n<M.length;n++){  
            if(M[i][n]==1) q.offer(new int[]{i,n});  
        }  
        set.add(i);  
        while(!q.isEmpty()){  
            int[] tmp = q.poll();  
            M[tmp[0]][tmp[1]] = 0;  
            M[tmp[1]][tmp[0]] = 0;  
            set.add(tmp[1]);  
            for(int k=0;k<M[0].length;k++){  
                if(tmp[1]!=k && M[tmp[1]][k]==1){  
                    q.offer(new int[]{tmp[1],k});  
                }  
            }  
        }  
    }  
}

这样可以做，但是比较耗时，下面的大佬的解法；
其实不用遍历矩阵，因为总人数都知道的，并且两个人是互为朋友的，可以建立一个boolean数组，表示第i个人有没有加入朋友圈，没有的话就进行一次搜索，并将i置为true，每次搜索会将同一个朋友圈的人都置为true，因此搜索的次数就是朋友圈的数量：

class Solution {  
    public int findCircleNum(int[][] M) {  
        boolean[] record = new boolean[M.length];  
        int count = 0;  
        for(int i=0;i<M.length;i++){  
            if(!record[i]){  
                search(M,record,i);  
                count++;  
            }  
        }  
        return count;  
    }  
    public void search(int[][] M,boolean[] record,int i){  
        for(int k=0;k<M.length;k++){  
            if(M[i][k]==1 && !record[k]){  
                record[k] = true;  
                search(M,record,k);  
            }  
        }  
    }  
}

大佬不愧是大佬！

NO.576 出界的路径数

给出一个矩阵的大小，一个最大步数，一个位置坐标，从这个坐标开始，每次可以向上下左右走一步，走出矩阵边界则是一条出界路径，求所有的出界路径数；
一开始直接写DFS，结果超时，毕竟结果的数值这么大，没有想到更好的剪枝策略；记忆化搜索有点动态规划的思想，将之前的结果保存起来便于计算以减少耗时，这里是用一个HashMap记录，而HashMap的key为int[]又比较麻烦，值相同引用不同，于是就将i,j,N转换成字符串（这里需要注意以下记忆化搜索的使用，和动态规划的思想很像）：

class Solution {  
    Map<String,Integer> map = new HashMap<>();  
    public int findPaths(int m, int n, int N, int i, int j) {  
        //map保存的是从[i,j]走到[x,y]后剩余步数为N再走到边界的路径数  
        return dfs(m,n,N,i,j);  
    }  
    public int dfs(int m,int n,int N,int i,int j){  
        if(N<0) return 0;  
        if(N<i+1 && N<j+1 && N<m-i && N<n-j) return 0;  
        if(i<0 || i>=m || j<0 || j>=n){  
            return 1;  
        }  
        if(map.containsKey(i+","+j+","+N)){  
            return map.get(i+","+j+","+N);  
        }  
        int count = 0;  
        count = (count+dfs(m,n,N-1,i+1,j))%1000000007;  
        count = (count+dfs(m,n,N-1,i-1,j))%1000000007;  
        count = (count+dfs(m,n,N-1,i,j+1))%1000000007;  
        count = (count+dfs(m,n,N-1,i,j-1))%1000000007;  
        map.put(i+","+j+","+N,count);  
        return count;  
    }  
}

NO.695 岛屿的最大面积

给定一个矩阵包含0和1，其中1表示陆地，0表示海水，找出矩阵中最大的岛屿面积；
对于这个问题就需要从某个为1的位置开始DFS，对于每个位置搜索其上下左右四个方向，并将一块陆地的面积累加；

class Solution {  
    public int maxAreaOfIsland(int[][] grid) {  
        int max = 0;  
        for(int i=0;i<grid.length;i++){  
            for(int j=0;j<grid[0].length;j++){  
                if(grid[i][j]==1){  
                    max = Math.max(max,backtrack(grid,i,j));  
                }  
            }  
        }  
        return max;  
    }  
    public int backtrack(int[][] grid,int i,int j){  
        if(i<0 || i>=grid.length || j<0 || j>=grid[0].length || grid[i][j]!=1) return 0;  
        int sum = 1;  
        grid[i][j] -= 1;  
        sum += backtrack(grid,i,j+1)+backtrack(grid,i+1,j)+backtrack(grid,i,j-1)+backtrack(grid,i-1,j);  
        // grid[i][j] += 1;  //不用还原，遍历过的位置就不用再遍历了  
        return sum;  
    }  
}

NO.79中遍历过的字符需要还原是因为该字母之后还可能会用到，而本题中遍历过的位置之后不用再遍历；

NO.5406 收集树上所有苹果的最少时间

给定一个二维数组，n个数都是在0到n-1之间，其中[i,j]表示i连向j，因此这个二维数组可以看作，因此每个数可以看作一个节点，二维数组表示节点之间的连接，此外还有一个boolean数组hasApple，hasApple[i]表示第i个节点是一个苹果，要求的是如果要摘下这棵树的所有苹果，需要走的最短路径是多少？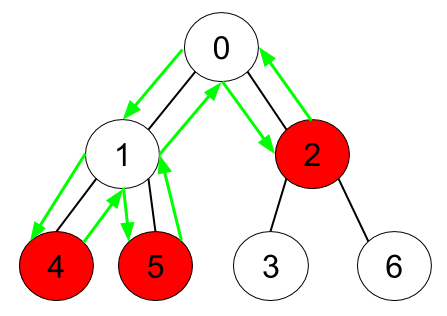

一开始是想求出每个苹果节点的深度，但是有的节点是会共用一条路径的，所以单纯求深度不行，要保证路径不会重复使用，想来想去只能用递归之前只会用无返回值的dfs，这里直接返回结果的想了很久，而且一开始是用二维list，每个位置i保存i的下一个数，但是光建立list都要O(n^2)时间，因此一直超时，后来才发现可以用HashMap，只需要O(n)时间建表：

class Solution {  
    Map<Integer,List<int[]>> map = new HashMap<>();  
    public int minTime(int n, int[][] edges, List<Boolean> hasApple) {  
        for(int[] l: edges){  
            List<int[]> list = new ArrayList<>();  
            if(map.containsKey(l[0])){  
                list = map.get(l[0]);  
                list.add(l);  
            }else{ list.add(l);}  
            map.put(l[0],list);  
        }  
        return 2*traverse(hasApple,0);  
    }  
    //计算获取一棵子树里的所有苹果所需要的最短路径长度，如果子树只有一个节点返回0；  
    //对于根节点n的每个子节点i，加上递归求解子树i的结果  
    public int traverse(List<Boolean> hasApple,int i){  
        //如果越界或i是叶子节点没有子节点，返回0；  
        if(!map.containsKey(i)) return 0;    
        int count = 0;  //收集以i为根节点的子树最短路径长度  
        for(int[] k: map.get(i)){  //遍历i的每一个子节点  
            int tmp = traverse(hasApple,k[1]);  //对子节点递归求解  
            if(tmp>0){  //如果子树上有苹果，加上路径长度+1  
                count += tmp+1;  
            //否则，如果子树只有一个节点。且该节点是一个苹果则+1  
            }else if(hasApple.get(k[1])){    
                count += 1;  
            }  
        }  
        return count;  
    }  
}

NO.面试题17.22 单词转换

给定两个单词beginWord和endWord，和一个单词表wordList，要将beginWord转换为endWord，要求每次只能变动一个字母，并且每次变动的结果要在单词表中，返回单词变换的过程，如：["hit","hot","dot","lot","log","cog"]；
这个问题相当于在一个图上找两个点之间的一条路径，也可以看作一颗树上的节点，因此可以使用DFS来做，关键在于只需要返回一个结果，如果还是遍历所有结果那么就会超时了；
思路一：对每个单词找到其所有可以转换的单词，存放在HashMap中，然后使用DFS，这样做在建立HashMap的时候比较费时间；思路二：不建立HashMap，每次都遍历wordList寻找下一个可以转换的单词；定义dfs()方法的作用就是根据单词表wordList返回beginWord到endWord的变换过程，因此是一个递归的过；

class Solution {  
    public List<String> findLadders(String beginWord, String endWord, List<String> wordList) {  
        if(!wordList.contains(endWord)) return new ArrayList<>();  
        return dfs(wordList,beginWord,endWord,new HashSet<>());  
    }  
    public List<String> dfs(List<String> wordList,String str,String end,Set<String> set){  
        if(str.equals(end)){  
            List<String> l = new ArrayList<>(){{add(str);}};  
            return l;  
        }  
        set.add(str);  
        for(String s: wordList){  
            if(!set.contains(s) && judge(str,s)){  
                List<String> result = dfs(wordList,s,end,set);  
                if(result.size()!=0){  //防止转换不存在  
                    result.add(0,str);  
                    return result;  
                }  
            }  
        }  
        return new ArrayList<>();  
    }  
    public boolean judge(String s1, String s2){  
        if(s1.length()!=s2.length()) return false;  
        int count = 0;  
        for(int i=0;i<s1.length();i++){  
            if(s1.charAt(i)!=s2.charAt(i)){  
                count++;  
            }  
            if(count>1) return false;  
        }  
        return count!=0;  
    }  
}

Java-BFS与DFS

1.组合总数问题

NO.39 组合总数

NO.40 组合总数II

NO.216 组合总数III

NO.377 组合总数IV

2.图的拓扑排序

NO.210 课程表II

3.八皇后等问题

NO.37 解数独

NO.51 N皇后

其他的DFS与回溯问题

NO.17 电话号码的字母组合

NO.78 子集

NO.79 单词搜索

NO.93 复原IP地址

NO.131 分割回文串

NO.200 岛屿数量

NO.322 零钱兑换

NO.337 打家劫舍III

NO.417 太平洋大西洋水流问题

NO.473 火柴拼正方向

NO.542 01矩阵

NO.547 朋友圈

NO.576 出界的路径数

NO.695 岛屿的最大面积

NO.5406 收集树上所有苹果的最少时间

NO.面试题17.22 单词转换

Related Posts

Java-动态规划算法

Machine-Learing：GBDT与XGBoost

数据结构：字典(Trie)树的实现(Java)

Java-BFS与DFS

1.组合总数问题

NO.39 组合总数

NO.40 组合总数II

NO.216 组合总数III

NO.377 组合总数IV

2.图的拓扑排序

NO.210 课程表II

3.八皇后等问题

NO.37 解数独

NO.51 N皇后

其他的DFS与回溯问题

NO.17 电话号码的字母组合

NO.78 子集

NO.79 单词搜索

NO.93 复原IP地址

NO.131 分割回文串

NO.200 岛屿数量

NO.322 零钱兑换

NO.337 打家劫舍III

NO.417 太平洋大西洋水流问题

NO.473 火柴拼正方向

NO.542 01矩阵

NO.547 朋友圈

NO.576 出界的路径数

NO.695 岛屿的最大面积

NO.5406 收集树上所有苹果的最少时间

NO.面试题17.22 单词转换

Share :

Related Posts

Java-动态规划算法

Machine-Learing：GBDT与XGBoost

数据结构：字典(Trie)树的实现(Java)